[고전역학 | Mechanics] 13. 중력

# 뉴턴의 중력 법칙

 

우주에 존재하는 물질의 모든 입자는 다른 모든 입자를 그 입자들의 질량의 곱에 비례하고 그들 사이의 거리의 제곱에 반비례하는 힘으로 서로 잡아당긴다. 이를 중력 법칙(law of gravitation)이라 하며 다음과 같이 표현할 수 있다.

 

 

이때 G는 중력상수(gravitational constant)라 불리는 물리상수이다.

중력은 항상 두 물체를 연결하는 선상에서 작용하며, 작용-반작용의 쌍을 이룬다.

 

 

 

 

중력상수 G값을 결정하기 위해 뒤틀림 저울을 활용할 수 있다.

 

 

 

 

 

 

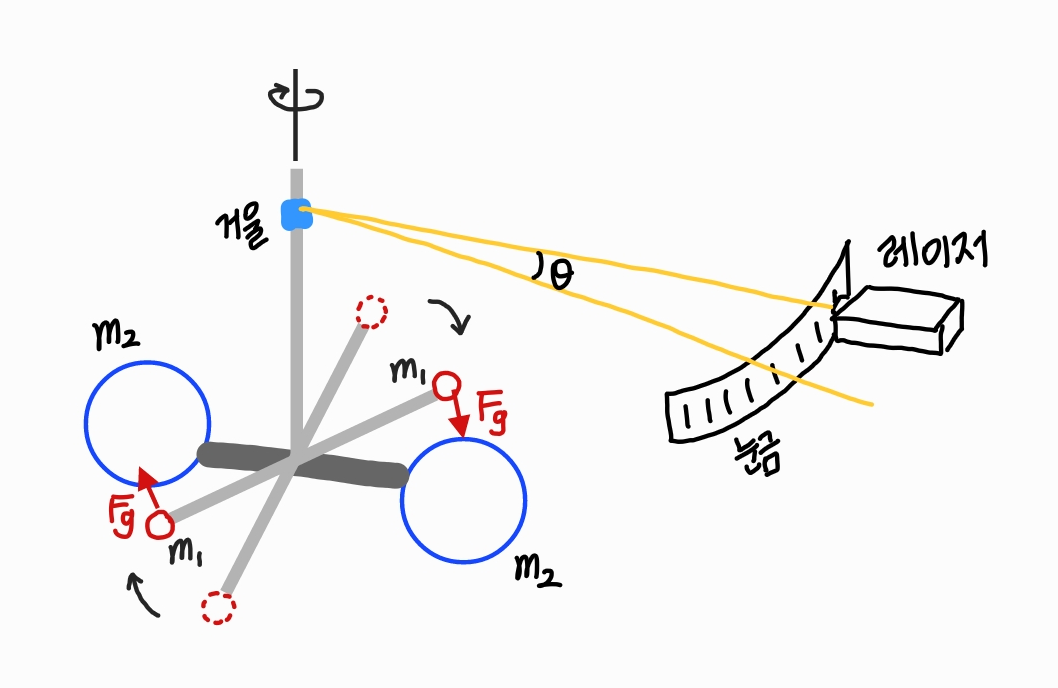
뒤집힌 T자 형태의 가볍고 단단한 막대가 아주 얇은 연직의 수정섬유에 의해 매달려 있으며, 질량이 각각 m₁인 두 개의 작은 구가 T자 막대의 수평 팔 끝에 부착되어 있다.

 

이때 질량이 각각 m₂인 두 개의 큰 구를 접근시키면 인력에 의해 T자 막대가 작은 각도로 비틀어진다.

 

이 각도를 측정하기 위해 T자 막대에 고정된 거울에 빛을 비춘다.

이때 거울에서 반사된 빛이 눈금에 비추어지는데, T자 막대가 뒤틀림에 따라 반사된 빛은 이 눈금을 따라 움직인다.

 

이를 활용하여 중력상수 G값을 구하면 다음과 같다.

 

 

 

 

 

 

 

 

 

 

 

 

 

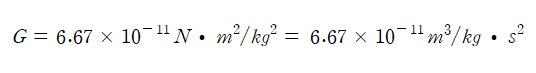
# 중력과 중첩원리

여러 개의 입자가 있을 때, 그중 한 입자에 나머지 입자가 작용하는 알짜 중력은 중첩원리를 이용하여 구한다.

즉, 먼저 한 입자에 다른 입자가 작용하는 중력을 차례대로 계산하여 이 값들을 모두 벡터 합하여 구할 수 있다.

 

상호작용하는 n개의 입자 중에 입자 1에 작용하는 중력에 대한 중첩원리는

 

 

 

 

 

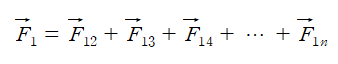
이다. 이를 간단하게 표기하면 다음과 같다.

 

 

 

 

유한한 크기의 물체가 한 입자에 작용하는 중력을 구하기 위해서는 물체를 미소 요소로 나누어 입자와 미소 요소 간의 힘들을 모두 벡터 합한다.

 

따라서 위의 식을 적분으로 확장하여 표현할 수 있다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

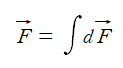
# 지표면 근처의 중력

지구를 질량 M인 균일한 공이라 가정하고, 질량 m의 입자가 지구 중심에서부터 거리 r만큼 떨어진 외부에 있는 경우에 대해 생각한다.

 

중력 법칙으로부터

 

 

 

 

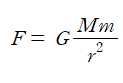
의 식을 구할 수 있다.

 

 

이때 입자를 놓아주면 입자에는 중력 F가 작용하게 되고, 입자는 중력가속도 g로 지구 중심을 향해 떨어진다.

뉴턴 제 2법칙으로부터 F=mg이므로, 중력 법칙 식으로부터 구한 중력가속도는 다음과 같다.

 

 

 

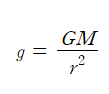
따라서, 지표면으로부터의 고도가 0km인 경우의 중력가속도는 9.8m/s² 임을 구할 수 있다.

 

그러나 이러한 값을 실제 중력가속도와 완전히 일치하지 않는데, 이는 실제로 지구는 공 모양이 아니며, 질량이 균일하게 분포되어있지도 않기 때문이다.

 

또한, 지구는 자전하고 있기에 지표면 상의 물체는 지구에 의한 중력과 지구의 자전으로 인한 구심력이 작용한다.

 

지구가 각속력 w로 자전할 때, 지구 위의 물체에 작용하는 힘은 다음과 같다.

 

 

 

 

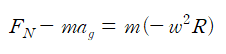
물체에 작용하는 수직항력은 저울로 측정한 물체의 무게 mg와 같다. 즉,

 

 

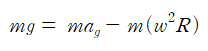
이며 측정된 무게는 지구의 자전으로 인해 실제보다 작게 측정된다.

또한 위 식의 양변을 질량으로 나눈다.

 

 

 

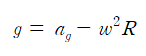
즉, 자유낙하 가속도는 지구의 자전으로 인해 실제보다 작게 측정된다.

 

지구의 24시간에 한 바퀴(2πrad)를 회전하므로 각속력 w를 구할 수 있다. 이는 아주 작은 값(0.032m/s²)이므로 무시하여 계산한다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 지구 내부에서의 중력

지구의 밀도가 균일한 경우, 어떤 입자에 작용하는 중력은 지면에서 최대가 되고 바깥으로 갈수록 감소한다.

 

만약 입자가 깊은 수직 갱도를 따라서 지구 안으로 들어간다면 중력에는 두 가지 요인이 작용하게 된다.

 

먼저, 지구중심에 좀 더 가까이 왔으므로 중력이 증가하는 경향을 띠게 된다.

그러나 입자의 위치 밖에 있는 질량 요소는 더 이상 입자에 중력을 작용하지 않으므로 중력은 감소하는 경향을 띠게 된다.

 

 

 

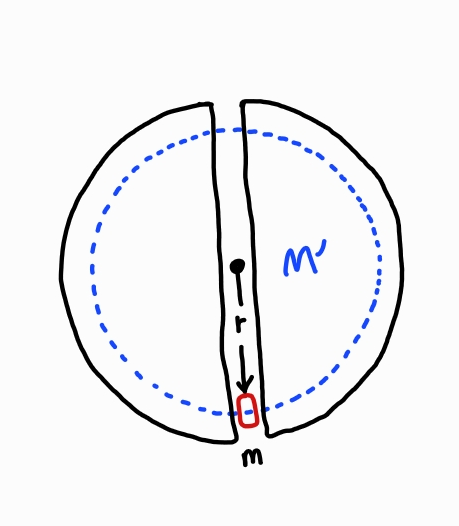
이는 위의 그림과 같은 상황에서 물체가 지구 중심 반지름으로부터 r인 위치에 있을 때, 물체에 가해지는 중력은 반지름 r이고, 질량이 M’인 작은 지구가 공에 가하는 중력과 같다는 의미이다.

 

따라서 반지름 r인 작은 지구 바깥 부분의 질량 요소들은 물체에 아무런 영향을 주지 않으며, 물체가 지구 내부에 가까워짐에 따라 작은 지구의 반지름도 감소하고 작은 지구의 질량도 감소하게 된다.

 

두 가지의 상반된 요인이 변화함에 따라 어느 요인이 더 큰 영향을 미치는지 알아본다.

 

 

지구의 질량이 균일하게 분포되었다면 반지름의 감소가 더 큰 영향을 미친다.

즉, 지구 중심에 가까이 접근함에 따라 중력은 서서히 감소하여 0이 된다.

 

그러나 실제 불균일한 지구의 경우 입자가 지구 내부로 들어가기 시작할 때는 중력이 증가하다가 어떤 깊이에서 최대에 도달하고 그다음부터 감소하기 시작한다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 중력 위치 에너지

지구 위에서 야구공을 수직으로 쏘아 올릴 때, 그 경로를 따라 지구 중심에서 R의 거리에 있는 점 P에서 그 공의 중력 퍼텐셜에너지 U를 계산한다.

 

 

 

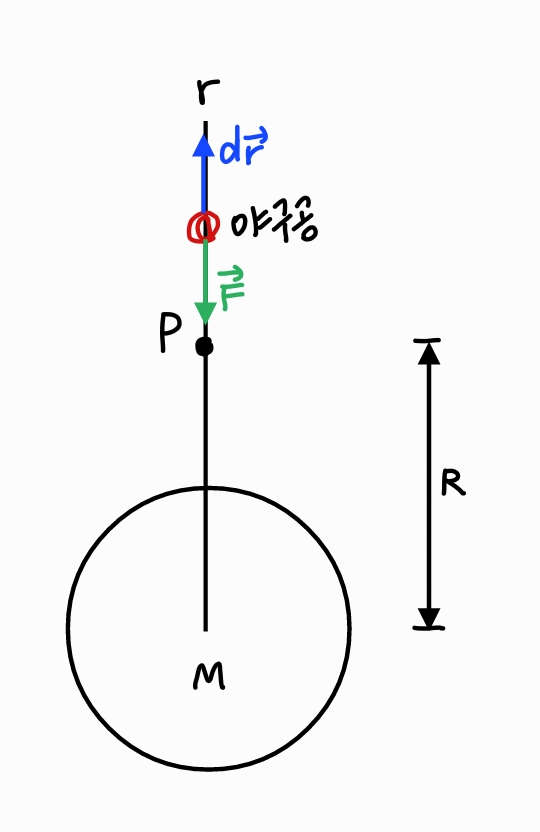
이는 공이 점 P에서 지구로부터 무한히 먼 거리까지 갈 때 중력이 공에 한 일 W를 계산하여 구할 수 있다.

 

중력은 떨어진 거리 r에 의해 변화하는 값이기 때문에 적분을 활용하여 다음과 같이 나타낼 수 있다.

 

 

 

벡터 곱은

 

 

 

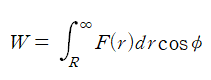
와 같이 나타낼 수 있다. 여기서 각 ϕ는 F(r)과 dr의 사잇각으로, 180°를 대입하여 계산한다.

 

 

 

여기서 M은 지구의 질량이고 m은 공의 질량이다. 위 식을 적분하면,

 

 

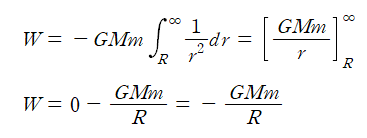
이며, 이 값은 공을 점 P에서 무한대로 보내기 위한 값이다.

한편 ⧍U=-W이므로, 다음과 같이 일을 퍼텐셜 에너지로 바꾸어 표기할 수 있다.

 

 

 

무한대에서 퍼텐셜에너지는 0이고 U는 P에서의 퍼텐셜에너지이므로 중력 퍼텐셜 에너지는

 

 

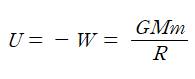
이다.

 

만일 계가 두 개 이상의 물체를 포함하면 차례로 쌍을 택하여 다른 물체는 없는 것처럼 가정하고 각 쌍의 퍼텐셜에너지를 계산한 후 모두 합하여 구할 수 있다.

 

예를 들어, 질량이 각각 m₁, m₂, m₃인 세 개의 입자가 있는 경우의 퍼텐셜에너지는 다음과 같다.

 

 

 

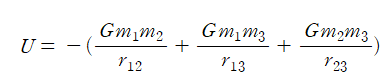
이번에는 야구공의 위치가 점 P에서부터 무한히 먼 거리가 아닌 지구 중심으로부터 거리 r₁에서 r₂로 이동하는 경우를 생각한다.

 

이러한 경우, 앞의 식을 그대로 사용하여 적분 범위만 다르게 계산한다.

 

 

 

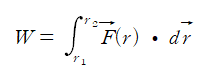
이고,

 

 

 

이다.

위 식으로부터 중력 퍼텐셜에너지는 오로지 처음과 끝의 r에 의존하며 경로에 무관하다.

 

 

 

따라서 중력은 항상 보존적이다.

 

위에서 구한 중력 퍼텐셜에너지에 일반적인 에너지 관계를 적용한다.

일하는 유일한 힘이 물체에 작용하는 중력인 경우, 계의 총 역학적 에너지는 일정하다.

즉, 역학적 에너지 보존 법칙을 적용하여 물체가 행성을 완전히 벗어나기 위한 속력인 탈출 속력을 계산할 수 있다.

 

 

 

 

탈출 속력 v로 행성의 표면을 떠나는 질량 m인 물체를 생각해본다.

 

물체는 무한대 위치에서 정지하므로 이때 운동에너지는 없다.

또한, 무한대 위치에서 퍼텐셜에너지는 0이므로 이때의 총 역학적 에너지는 0이 된다.

따라서 행성의 표면에서도 총 역학적 에너지는 0이 되어야 한다.

 

 

탈출 속력 v는 발사되는 방향과는 무관한 값을 갖는다. 그러나 행성의 자전을 고려하여 발사대가 움직이는 방향으로 발사하면 탈출 속력을 더 쉽게 얻을 수 있다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 케플러 법칙과 행성의 운동

Kepler로부터 발견된 행성의 운동법칙은 다음과 같다.

1. 궤도 법칙: 모든 행성은 태양을 하나의 초점으로 하는 타원궤도로 운동한다.

 

 

타원은 두 개의 초점을 갖는다. 그중 한 초점 S에 태양이 위치한다.

 

타원의 중심에서 각 초점까지의 거리는 타원의 장축의 절반과 이심률(eccentricity)의 곱 ea로 구할 수 있다. 이심률이 0일 때 타원은 원이 된다.

 

행성의 궤도에서 태양에 가장 가까운 점을 근일점(perihelion)이라 하고, 태양에서 가장 먼 점을 원일점(aphelion)이라 한다.

 

뉴턴은 뉴턴 법칙과 중력법칙, 미분 방정식을 응용하여 1/r²에 비례하는 인력이 작용하는 물체의 유일한 닫힌 궤도는 원이나 타원뿐인 사실을 증명하여 케플러 제 1법칙을 증명하였다.

또한, 1/r²에 비례하는 인력이 작용하는 물체의 열린궤도의 궤적은 포물선이나 쌍곡선이라는 것도 증명할 수 있었다.

 

 

 

 

2. 면적 법칙: 행성과 태양을 연결하는 선분은 같은 시간 동안 같은 면적의 궤도면을 휩쓸고 지나간다. 즉 면적 dA를 휩쓸고 지나가는 비율 dA/dt는 일정하다.

 

 

 

 

 

 

 

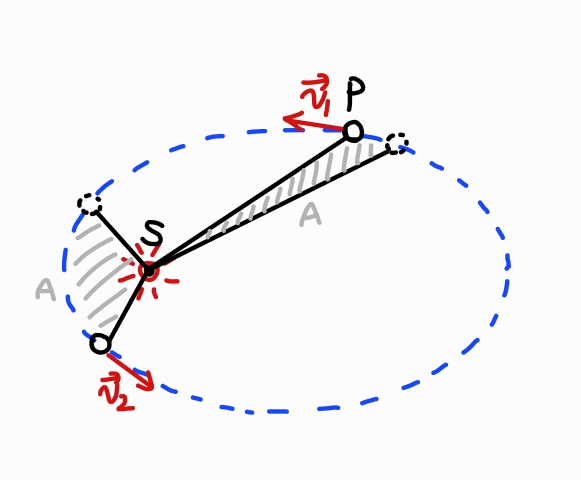
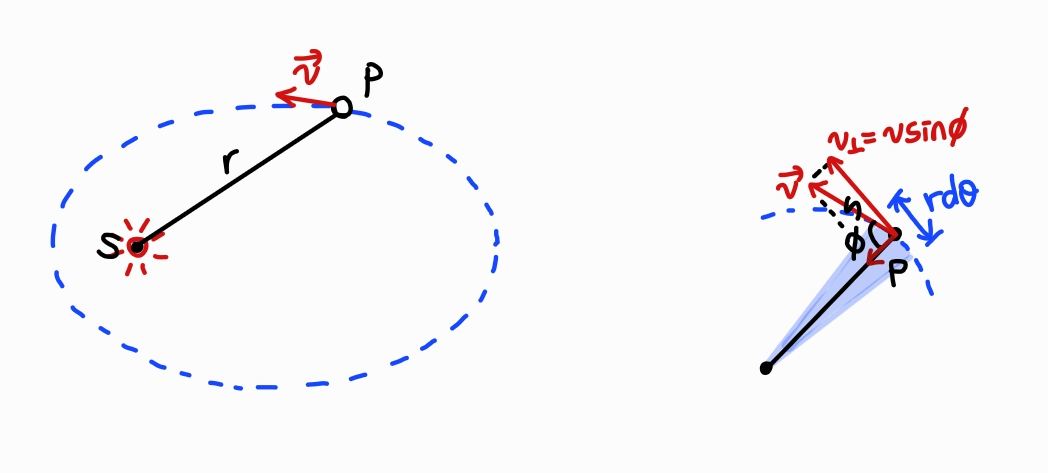
작은 시간 간격 dt동안 태양 S에서 행성 P에 이르는 직선은 각도 dθ만큼 회전한다.

이 직선이 휩쓴 면적은 높이 r, 밑변 길이 rdθ인 색칠한 삼각형의 넓이로 근사하여 계산할 수 있다.

 

 

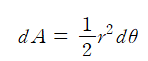
양변을 t에 대해 미분하면, 시간에 대한 면적 변화율 dA/dt를 면적 속도라 하며

 

 

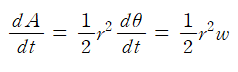
와 같이 나타낼 수 있다. 이때 w는 태양과 행성을 잇는 선분의 각속력이다.

 

 

 

또한 타원궤도 상에서 각운동량을 구하면,

 

 

위 식을 앞에서 구한 면적 속도식에 대입하여 나타낼 수 있다.

 

 

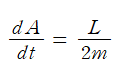
면적 속도 dA/dt가 일정하면 L도 일정한 값을 갖게 되므로 각운동량이 보존된다.

 

 

 

 

 

3. 주기 법칙: 행성 주기의 제곱은 행성 궤도 장축의 세제곱에 비례한다.

 

먼저 반지름 r인 원 궤도를 가정한다. 원 궤도상에서 운동하는 행성에 뉴턴 제 2법칙을 적용하면,

 

 

 

이다.

이때, 원 궤도 운동의 주기 T는 T=2π/w와 같이 나타낼 수 있으므로 각속력 w는 w=2π/T로 표현할 수 있다.

이 식을 위의 제 2법칙으로부터 구한 위의 식에 대입하여 다시 나타내면,

 

 

 이다.

 

 

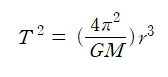
원 궤도 반지름 r값은 장축 a인 타원궤도에 대응하며, 이는 뉴턴이 증명하였다.

 

 

 

 

 

지금까지의 모든 행성 운동은 태양은 정지한 상태로 가정하여 계산한 결과이다.

그러나 실제로 태양과 행성은 모두 질량 중심 주위를 공전한다.

 

 

그러나 이러한 효과를 무시하여 계산하더라도 결과값의 오차는 크지 않다.

이는 태양의 질량이 다른 행성들의 질량 합에 비해 매우 큰 값을 가지므로 태양계 질량 중심은 태양의 중심에서 멀지 않은 곳에 위치하기 때문이다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 인공위성의 운동

 

 

 

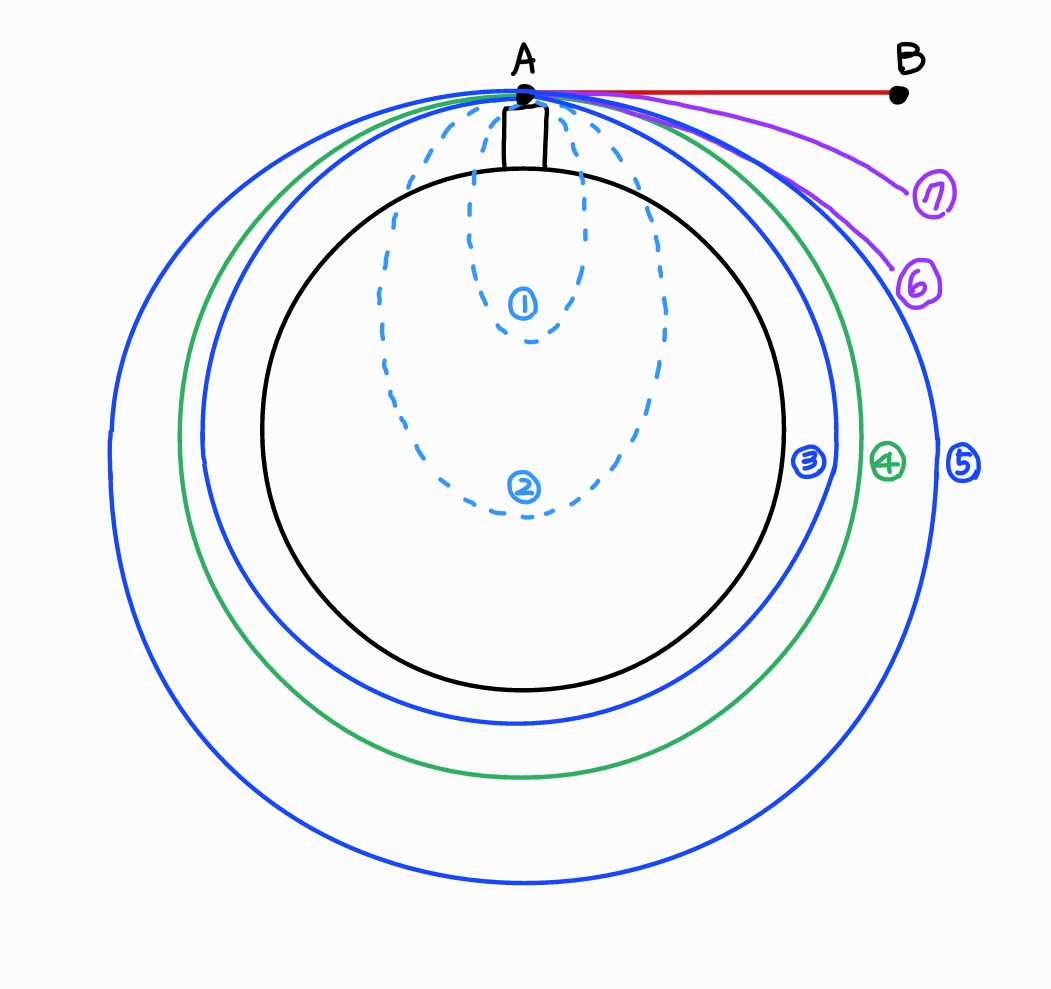
지구상의 점 A에서 지표면의 접선인 AB방향으로 포사체를 발사하는 경우를 생각한다.

 

초기 속력이 증가함에 따라 포사체의 궤도는 ①에서 ⑦로 변화한다. 궤적 ③에서부터 ⑤까지의 경우 포사체는 지표면을 벗어나 지구 위성이 된다.

 

만일 포사체에 속력을 늦추게 하는 힘이 작용하지 않는다면 포사체가 지구 주위를 한 바퀴 돌아 다시 A점에 되돌아왔을 때의 속력은 포사체의 초기 속력과 같고 포사체는 이러한 운동을 끝없이 계속한다.

 

궤적 ①부터 ⑤까지는 모두 닫혀 있으며, 이들은 닫힌 궤도(closed orbit)라고 부른다. 모든 닫힌 궤도는 타원이거나 타원의 일부분이다. 궤적 ④는 타원의 특별한 경우인 원이다. 궤적 ⑥과 ⑦은 열린 궤도(open orbit)이다. 이러한 포사체는 시작점으로 다시 돌아오지 않으며 지구로부터 벗어난다.

 

 

 

 

궤적 ④와 같은 특별한 원 궤도의 운동을 분석한다.

 

원 궤도의 위성의 등속력을 v라 할 때, 위성의 구심 가속도의 크기는 v²/r이고, 항상 원의 중심을 향한다.

중력 법칙에 의해 질량이 m인 위성에 작용하는 중력은 GMm/r²이고 위성은 중력에 의한 힘으로부터 위성의 궤도를 유지하게 하는 구심 가속도를 제공한다.

 

 

즉, 뉴턴의 제 2법칙으로부터

 

 

이므로 이를 v에 대해 풀면

 

 

 

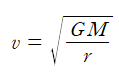
이다.

 

따라서 궤도 반지름 r과 위성의 속력 v는 각각 독립적으로 선택할 수 없으며, 궤도 반지름이 주어지면, 원형궤도에 대한 속력이 결정된다. 또한 위성의 속력은 위성의 질량 m에 무관한 값을 갖게 된다.

 

다음으로 원 궤도 반지름 r과 회전하는 데 절리는 시간인 주기 T 사이의 관계식을 유도한다. 위성의 선속력 v는 한 회전 동안에 진행하는 거리인 2πr을 주기 T로 나눈 값이다.

 

따라서

 

 

 

이다. 따라서 원 궤도를 운동하는 위성은 궤도의 반지름이 클수록 느린 속력과 긴 주기를 갖는다.

마지막으로, 원 궤도를 운동하는 위성에 역학적 에너지 보존 법칙을 적용한다.

 

 

 

원형궤도에서 총 역학적 에너지는 음의 값이고, 그 값은 위치 에너지의 절반이다.

 

한편 반지름 r 대신 타원의 장축 a를 대입하면 타원궤도에서의 총 역학적 에너지를 구할 수 있다.

 

 

 

 

 

 

 

 

 

 

 

 

 

# 뉴턴의 껍질 정리

뉴턴은 껍질 정리로부터 두 입자 사이의 중력을 두 구형 물체 사이의 중력으로 확장하여 적용할 수 있었다.

따라서 구형의 균일한 껍질 물질은 마치 모든 질량이 중심에 모여 있는 것처럼 외부의 입자를 끌어당긴다.

 

 

이를 증명하기 위해, 질량이 m인 점 입자가 총질량이 M인 얇은 구 껍질과 상호작용하는 경우를 생각한다.

 

먼저, 구 껍질 밖의 점 질량 m이 있다고 가정한다. 구 껍질의 중심에서 m을 잇고 직선 위에 중심을 둔 구 껍질 표면상의 한 고리를 생각한다. 고리를 이루는 모든 입자는 점 질량 m으로부터 모두 같은 거리 s만큼 떨어져 있다.

 

 

 

 

따라서 점 입자 m과 고리 안에 있는 한 입자 사이의 상호작용하는 중력 퍼텐셜 에너지는

 

 

 

와 같이 나타낼 수 있다.

 

고리의 모든 입자에 대한 중력 퍼텐셜 에너지 dU는 위의 식을 모든 입자들에 대하여 더한 값과 같다.

즉,

 

 

 

 

다음으로 고리의 질량 dM을 구한다.

 

구 껍질의 반지름은 R이므로, 고리의 반지름은 Rsinϕ이고, 원주는 2πRsinϕ이다.

또한, 고리의 너비는 Rdϕ이므로 고리의 면적 dA는 다음과 같다.

 

 

 

구 껍질의 총 질량 M에 대한 고리의 질량 dM의 비는 구 껍질의 총면적 A에 대한 고리의 면적 dA의 비와 같으므로

 

 

 

이다. 위 식을 dM에 대해 정리하여 위에서 구한 dU 식에 대입하면

 

 

 

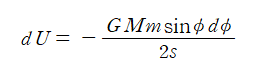
이다. 이 식은 점질량 m과 고리 사이의 상호작용에 의한 중력 퍼텐셜 에너지이다.

 

위 식을 고리가 아닌 구 전체로 확장하여 적용하기 위해서 각도 ϕ가 0에서부터 π까지, 거리 s를 r-R에서부터 r+R까지 변화시켜 적분한다.

 

 

ϕ와 dϕ를 s로 나타내기 위해 직각삼각형의 피타고라스 정리를 활용하여 관계식을 유도한다.

 

 

즉,

 

 

양변에 미분을 취한다.

 

 

이를 dU 식에 대입하면,

 

 

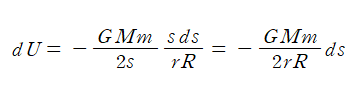
이를 s에 대해 r-R부터 r+R 까지 적분한다.

 

 

 

즉, 이 결과는 두 점 질량 m과 M이 거리 r만큼 떨어져 있을 때의 위치 에너지와 같다.

 

 

 

다음으로 점 질량 m이 구 껍질 내부에 있는 경우를 생각해본다.

 

 

 

 

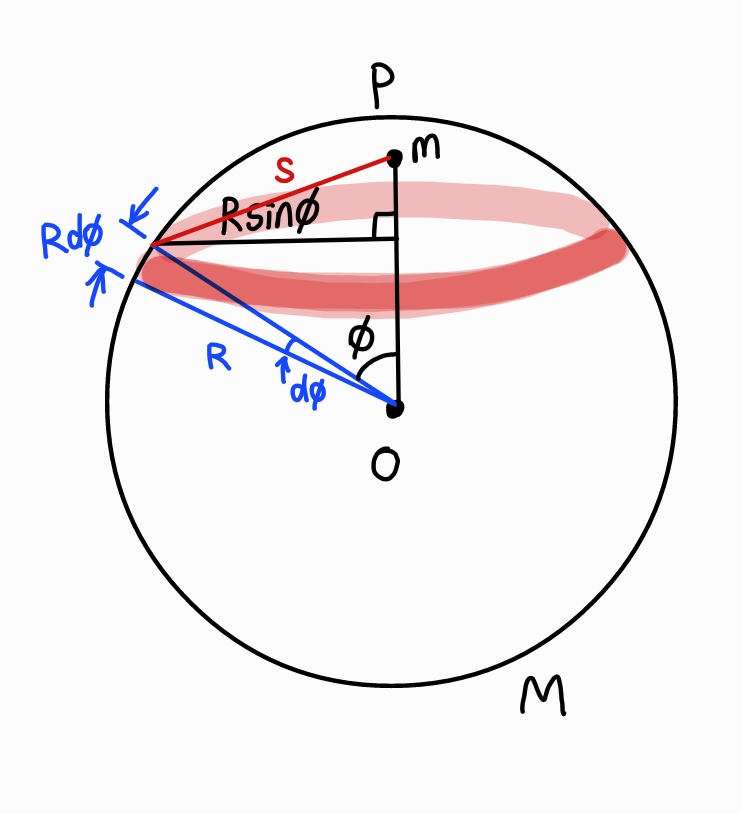
만약 점 질량 m이 구 내부에 있는 점이라면, 떨어진 거리 s는 R-r에서부터 R+r까지 변화한다.

 

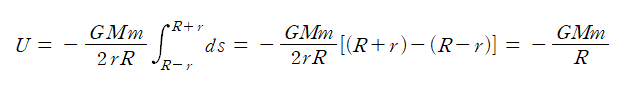
따라서, 점 질량 m이 구 내부에 있는 경우 내부의 어느 위치에서든지 같은 값을 갖는다.

 

 

 

 

 

 

 

 

 

 

 

참고문헌 : Young and Freedman, 대학물리학 12th ed, Haliday 일반 물리학 9th ed