[고전역학 | Mechanics] 02. 직선 운동

# 위치와 변위
물체의 위치는 어떤 기준점에 대한 상대적 위치로 나타낸다. 주로 원점을 기준으로 하여 양의 방향과 음의 방향을 나타낸다. 위치 x₁에서 다른 위치 x₂까지의 거리를 변위 ⧍x라 하고 다음과 같이 표기할 수 있다.

변위는 처음 위치와 나중 위치로 결정되므로 실제로 움직인 거리와는 상관이 없다.
예를 들어 입자가 x=5m에서 x=200m로 움직였다가 다시 5m의 위치로 되돌아온다면 출발점에서 도착점까지의 변위는 ⧍x = (5m) - (5m) = 0이다.
변위는 방향과 크기를 갖는 벡터로 부호를 표시하여야 한다.
# 평균속도와 평균속력
평균속도(average velocity)는 특정한 시간 간격 ⧍t와 그동안의 변위 ⧍x의 비율로 다음과 같이 정의한다.

x-t 그래프에서 평균속도는 곡선 x(t)위의 특정한 두 점을 연결하는 직선의 기울기이다.
한 점은 x₂와 t₂에 해당하고 다른 한 점은 x₁와 t₁에 해당한다. 변위와 마찬가지로 평균속도도 크기와 방향을 갖는 벡터이다.

평균속도의 크기는 직선 기울기의 크기이다.
평균속도에 관한 간단한 규칙은 다음과 같다.
x가 양수이면서 크기가 증가하고 있거나(➀), 음수이면서 절댓값이 줄어들고 있을 때(➁) 입자는 +x 방향으로 운동하고 있고, 평균속도는 양수이다. x가 양수이면서 크기가 감소하고 있거나(➂) 음수이면서 절댓값이 늘어나고 있을 때(➃) 입자는 -x 방향으로 운동하고 있고, 평균속도는 음수이다.


평균속력은 특정한 시간 간격 ⧍t와 그동안의 이동거리의 비율로 다음과 같이 정의한다.

평균속력은 방향을 포함하지 않기 때문에 부호가 없다.
# 순간속도와 순간속력
어느 순간의 속도는 시간 간격 ⧍t가 0에 접근할 때의 평균속도로 구할 수 있다. 이는 극한을 이용한 정의에 따라서
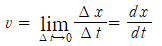
와 같이 나타낼 수 있다.
순간속도 v는 주어진 순간에 입자의 위치가 시간에 따라 변하고 있는 비율을 나타낸다. 즉, v는 t에 대한 x 미분이다. 또한 어느 순간의 v는 위치-시간 곡선에서 그 순간을 나타내는 점에서의 기울기임을 알 수 있다. 또한 순간속도도 벡터이므로 크기와 방향을 가진다. 순간속력은 순간속도의 크기이다. 즉, 속력은 방향을 무시한 속도와 같다.
# 가속도
속도가 위치의 시간에 대한 변화율을 나타냈던 것과 마찬가지로, 가속도는 속도의 시간에 대한 변화율을 나타낸다. 속도와 마찬가지로 가속도도 벡터이다. 평균 가속도와 순간가속도는 각각 다음과 같이 정의한다.
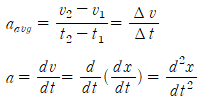
즉, 임의의 순간에서 입자의 가속도는 그 순간에서의 위치 함수의 시간에 대한 2차 미분이다.
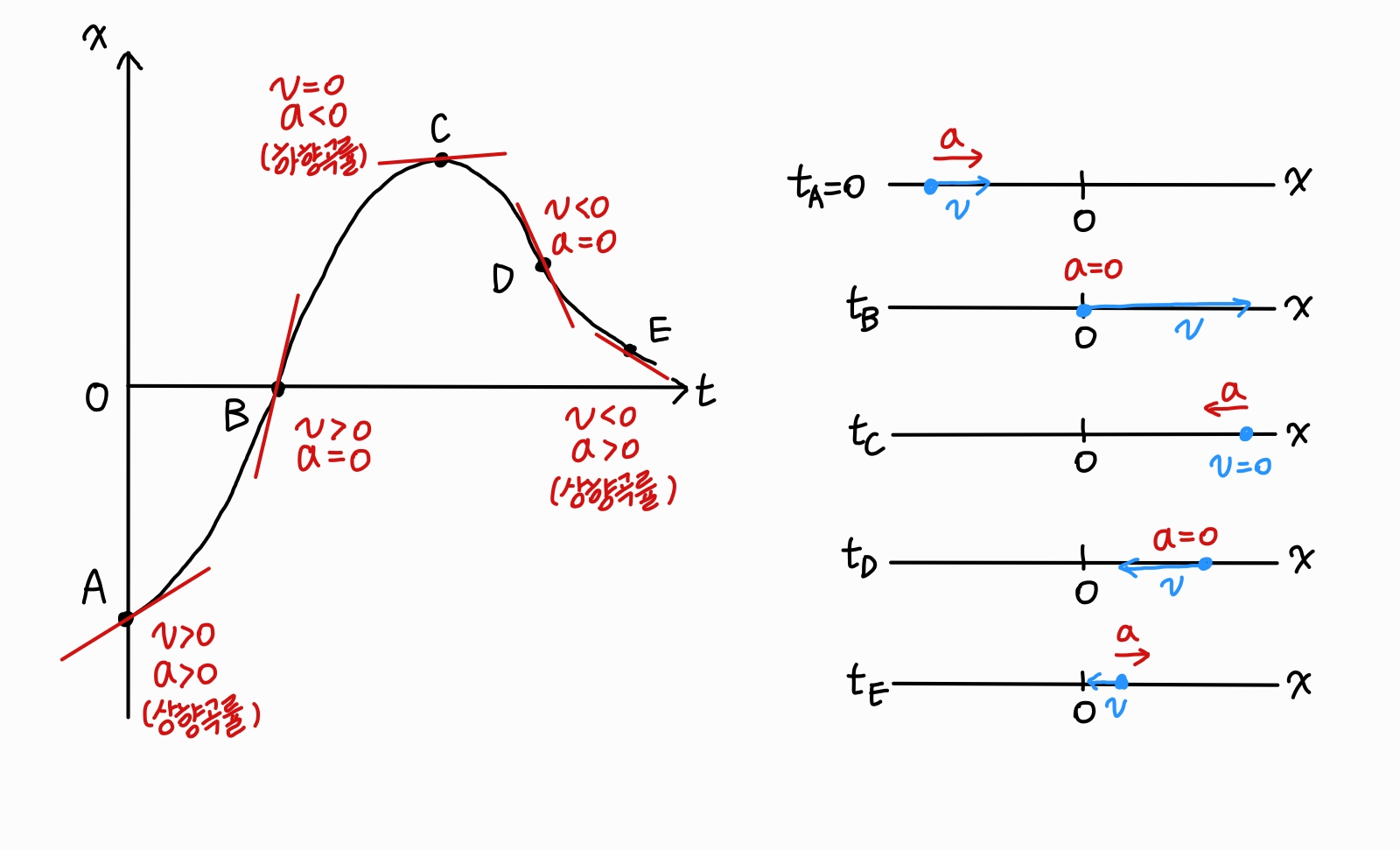
A에서 물체는 +x 방향으로 점점 빠르게 운동한다. B에서 물체는 원점에 위치하고 속력은 순간적으로 변하지 않다가 +x 방향으로 점차 느리게 운동한다. C에서 물체는 순간적으로 정지하며 –x 방향으로 막 움직이려 한다. 운동이 진행됨에 따라 –x 방향으로 점점 빠르게 운동한다. D에서 물체의 속력은 순간적으로 변하지 않는다. E에서 물체는 –x 방향으로 점차 느리게 운동하며 원점으로 근사한다.
입자의 운동은 위와 같이 왼쪽의 x-t 그래프와 오른쪽의 운동 도표(motion diagram)로 표현할 수 있다.
# 등가속도 운동
위의 그래프는 각각 등가속도 운동의 가속도, 속도, 위치 그래프이다.
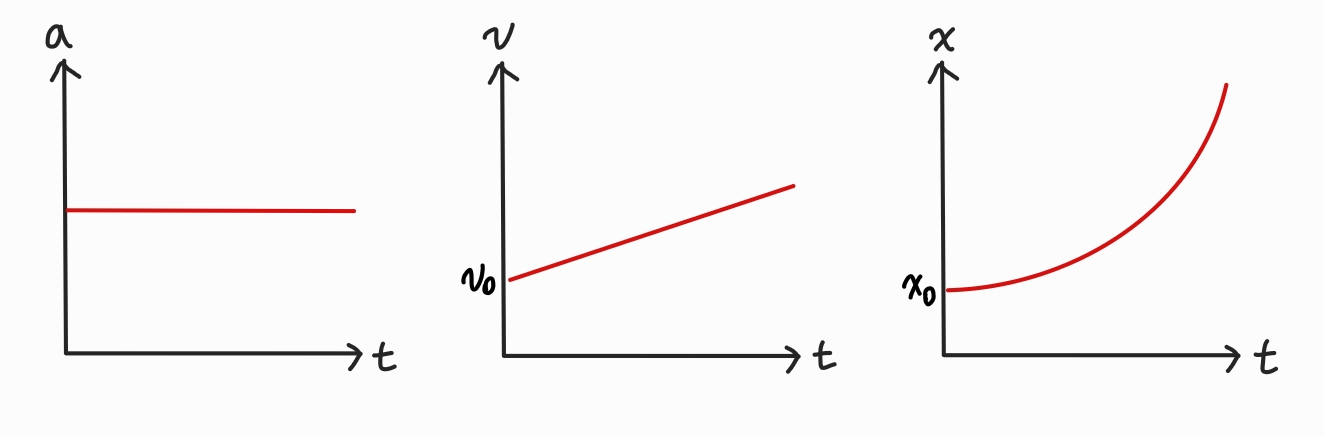
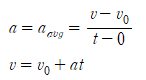
위 가속도-시간 그래프의 함수가 선형이므로 속도-시간 그래프는 직선으로 나타난다.
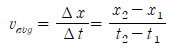
이므로

이다. 여기서 x₀는 시간 t = 0에서의 위치이고, v_{avg}는 시간 t = 0와 나중 시간 t사이의 평균속도이다.
선형 속도함수식인 위의 속도식에서 임의의 시간 간격(t = 0에서 나중 시간 t까지) 동안의 평균속도는 처음 속도와 마지막 속도의 산술 평균 이므로
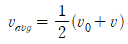
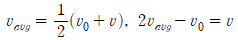
를 대입하여 정리하면,

이다. 이를 다시 x = x₀ + v_{avg}*t 에 대입하여 정리하면,

이다.
위 식에 t = 0을 대입하면 x = x₀임을 확인할 수 있다. 또한, 위 식을 미분하면 v = v₀ + at을 다시 얻을 수 있다.
위의 x = x₀ + v_{avg}*t 에 v_{avg} = 1/2 * (v₀ + v)을 대입하여 정리하면,

을 얻을 수 있다.
이 식에서 v = v₀ + at 을 이용하여 v₀를 소거한 식은 다음과 같다.

따라서, 등가속도 운동의 정의로부터 도출된 등가속도 운동의 기본 방정식은 다음과 같다.

다음으로, 시간 변수를 포함하지 않는 위치, 속도, 가속도 사이의 관계식을 구하고자 한다.
위에서 구한 방정식을 시간 t에 대한 표현으로 정리하면 다음과 같다.

x₀항을 좌변으로 옮기고, 양변에 2a를 곱하면

을 얻을 수 있고, 이를 정리하면

이다.
정리하면,
<등가속도 운동의 기본 방정식>
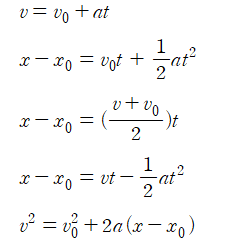
이다.
# 자유낙하
자유 낙하하는 물체의 일정한 가속도를 중력 가속도(acceleration due to gravity)라고 부르고, 그 크기를 g로 나타낸다. 지구 표면 혹은 근처에서 g의 값은 약 9.8m/s² 또는 980cm/s²이다. 중력 가속도의 정확한 값은 위치에 따라 변하므로 지구 표면에서 g의 값은 유효 숫자 두 자리까지 나타낸다. g는 벡터의 크기를 나타내기 때문에 항상 양(+)의 값이다.
달 표면에서의 중력 가속도는 g=1.6m/s² 이며, 태양표면 근처에서 중력 가속도는 g=270m/s²이다.
# 적분에 의한 속도와 위치 계산
물체의 가속도-시간 그래프를 적분하여 주어진 시간에서 물체의 속도를 구할 수 있다.
가속도 a가 a=dv/dt로 정의되므로 미적분학의 기본 정리에 의하여
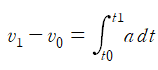
이다.
오른쪽 항은 정적분이며 v₀는 시간 t₀일 때의 속도이고, v₁는 나중 시간 t₁일 때의 속도이며, 다음과 같은 의미를 지닌다.

속도 v는 v=dx/dt로 정의하므로 같은 방법으로
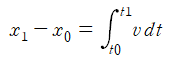
로 표기할 수 있다.
x₀는 시간 t₀일 때의 위치이고, x₁는 나중 시간 t₁일 때의 위치이며, 다음과 같은 의미를 지닌다.

참고문헌 : Young and Freedman, 대학물리학 12th ed, Haliday 일반 물리학 9th ed