[고전역학 | Mechanics] 07. 위치 에너지

# 중력 위치 에너지

물체의 위치 에너지(potential energy)는 물체가 그 위치에 있음으로써 얼마의 일을 할 수 있는지를 알려주는 능력 또는 가능성의 척도라고 할 수 있다. 어떤 물체가 공기저항이 없이 낙하하는 경우에서 중력에 의한 위치 에너지를 나타내는 식을 유도해 본다.

 

 

 

 

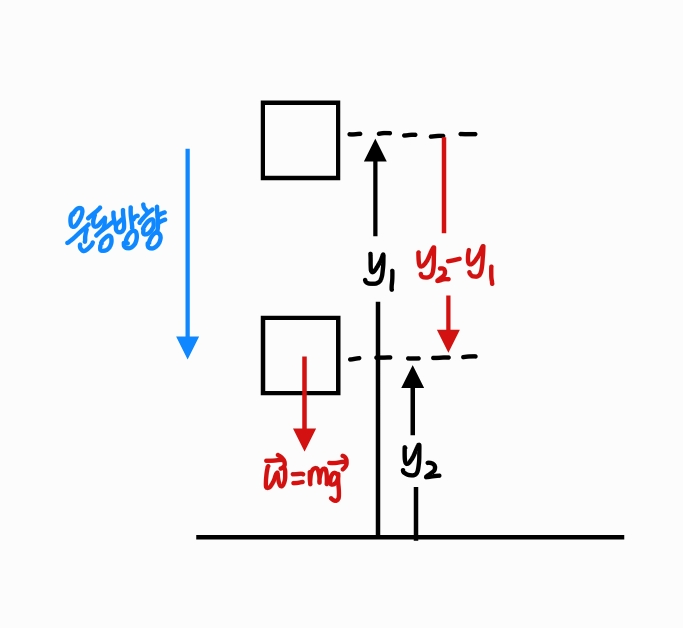
질량 m인 물체가 연직으로 놓인 y축 위에서 움직일 때, 이 물체에 작용하고 있는 힘은 크기가 w=mg인 물체의 무게이다.

물체가 지표면 가까이에 있으므로 물체의 무게는 일정하다. 물체가 높은 위치 y₁에서 낮은 위치 y₂로 떨어질 때 물체의 무게가 한 일을 계산한다. 무게의 방향과 변위의 방향이 같으므로, 무게가 물체에 해준 일 W는 양의 부호를 가지며

W = Fs = w(y₁ - y₂) = mgy₁ - mgy₂

와 같이 나타낼 수 있다.

 

 

 

 

 

물체가 위쪽으로 이동할 때도 위 식을 적용할 수 있는데, W는 무게와 변위의 방향이 반대이므로 음의 부호를 갖게 된다.

따라서, 중력이 한 일 W은 변위의 시점과 종점에서의 mgy값으로 표현할 수 있다. 이를 중력 위치 에너지(gravitational potential energy, U)라고 하며, 중력이 한 일은 중력 위치 에너지의 변화량으로써 표현할 수 있다.

 

 

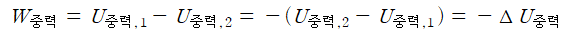
물체가 위로 움직이면 y는 증가하고 중력이 한 일은 음의 값을 갖게 되고 중력 위치 에너지는 증가하게 된다.

물체가 아래로 움직이면 y는 감소하고 중력이 한 일은 양의 값을 갖게 되고 중력 위치 에너지는 감소하게 된다.

위치 에너지의 단위로는 줄(joule, J)을 사용한다.

 

 

다음으로는 물체가 연직방향이 아닌 곡선이나 경사진 경로를 따라 움직이는 경우의 중력 위치 에너지를 계산해본다.

 

 

 

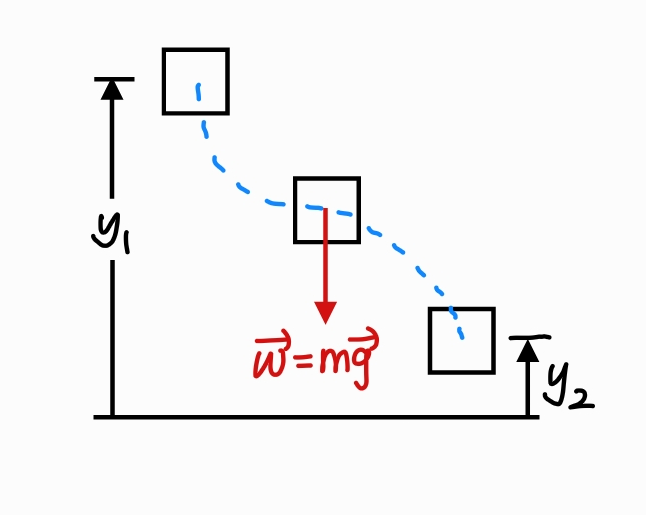
전체 경로를 ⧍s들로 나누어 해당 범위에서의 중력 위치 에너지를 계산하면, 중력이 한 일은 힘과 변위 두 벡터 간의 내적과 같다.

 

 

 

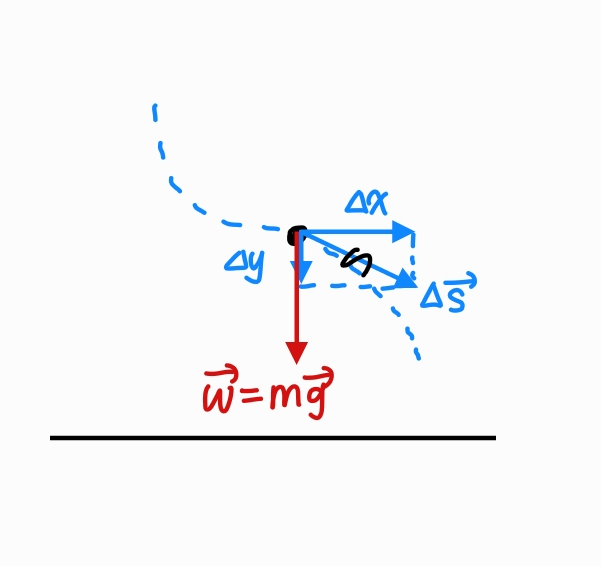
단위 벡터를 사용하여 표현하면,

힘은

 

이고, 변위는

 

 

 

가 되므로 두 벡터의 내적은

 

 

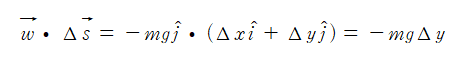
와 같다. 따라서 중력이 한 일은 물체가 수평으로는 움직이지 않고, 수직으로만 ⧍y만큼 움직인 경우와 같은 값을 가진다. 이것은 다른 모든 ⧍s 구간에서도 마찬가지이며 결국 중력이 한 일의 합은 –mg와 전체 변위 (y₂ - y₁)의 곱이 된다.

즉,

 

 

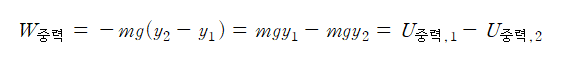
와 같으며, 이는 수직운동만 고려한 경우와 같은 값을 갖는다.

따라서 곡선 경로의 중력 위치 에너지에 대해서도 같은 식을 적용할 수 있다.

 

 

 

 

 

 

 

 

# 탄성 위치 에너지

용수철이나 고무줄과 같은 변형이 가능한 물체에 에너지를 저장하는 것을 탄성 위치 에너지(elastic potential energy)라 하며, 물체가 변형된 후 원래의 크기와 모양으로 되돌아 갈 수 있으면 이를 탄성이 있다고 말한다.

 

이상적인 용수철을 가정하고, 이 용수철이 늘어나는 경우에 대해 탄성 위치 에너지를 유도한다.

 

 

 

훅의 법칙(Hooke’s law)으로부터 이상적인 용수철을 잡아당기는 데 필요한 힘은 용수철이 늘어난 길이에 비례한다.

즉, 늘어난 길이 x가 너무 길지 않다면 용수철을 늘리는 데 필요한 힘은

 

F = kx

 

와 같이 나타낼 수 있으며, 이때 k는 상수이고 힘 상수(force constant) 또는 용수철 상수(spring constant)라고 부른다. k의 단위는 힘을 길이로 나눈 값으로 SI 단위에서 N/m와 같이 나타낸다.

 

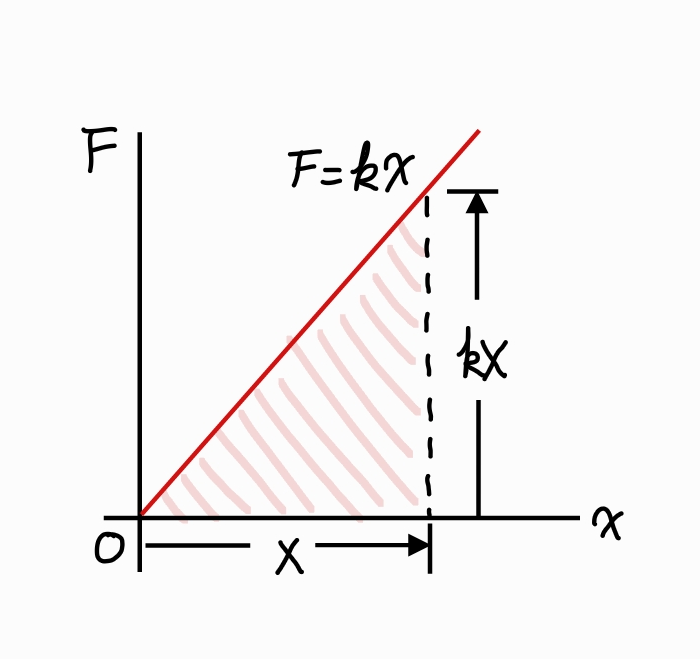
위 그림은 F를 늘어난 길이 x의 함수로 나타낸 그래프로서, 용수철이 늘어난 길이가 0에서 최대값 X에 도달할 때까지의 이 힘이 한 일은 그래프의 면적과 같은 값으로, 다음과 같이 나타낼 수 있다.

 

 

 

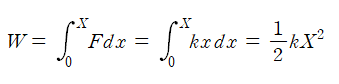
이 값은 평균 힘인 kX/2에 전체 변위 X를 곱한 값과 같으며, 위 식으로부터 전체 일은 용수철이 최종적으로 늘어난 길이 X의 제곱에 비례한다는 사실을 알 수 있다.

 

만일 용수철이 처음부터 이미 x₁만큼 늘어나 있었을 때, 그보다 더 길게 x₂만큼 늘리기 위한 일은 다음과 같다.

 

 

 

 

 

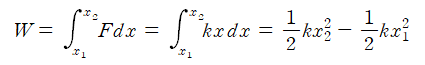
이는 위 그래프에서의 사다리꼴의 면적과 동일하다.

즉, 용수철에 해준 일은 다음과 같이 나타낼 수 있다.

 

 

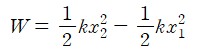
여기에서 용수철을 더 늘린다면 용수철에 양의 일을 가하여야 하며, 용수철을 줄어들도록 한다면, 음의 일을 용수철에 해주는 것과 같다.

 

다음으로 용수철이 한 일에 대해서 생각해본다. 용수철이 한 일은 뉴턴의 제 3법칙에 따라, 용수철에 해준 일의 반대 부호의 값을 갖게 된다. 따라서 변위가 x₁에서 x₂로 변하면 용수철이 하는 일은 위 식의 부호를 바꾸어,

 

 

와 같이 나타낼 수 있다.

 

 

 

 

 

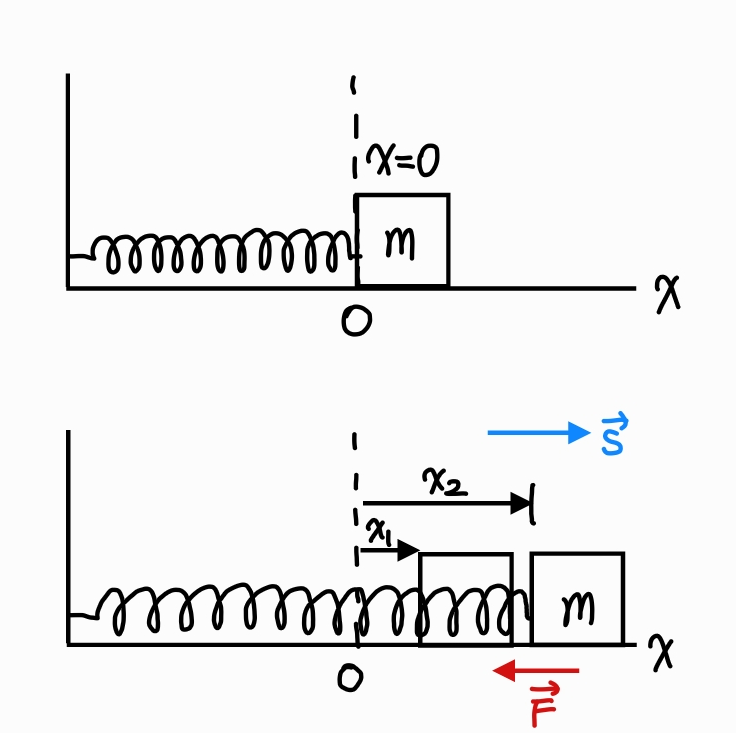
x₁과 x₂가 양의 값을 가지고 x₂가 x₁보다 큰 경우 물체가 +x방향으로 움직이는 동안 용수철이 –x방향으로 물체를 당기므로 용수철이 한 일은 음의 부호를 가진다. 용수철이 더 늘어날수록 물체의 속력은 줄어들며, 용수철에 저장되는 탄성 위치 에너지는 증가한다.

 

 

 

 

용수철을 압축시키는 경우 x₁또는 x₂ 또는 둘 다 음의 값을 가질 수 있으며, x₁가 x₂보다 큰 값을 가지므로 용수철이 한 일은 양의 부호를 갖는다. 그리고 용수철에 저장 되는 탄성 위치 에너지는 감소한다.

 

 

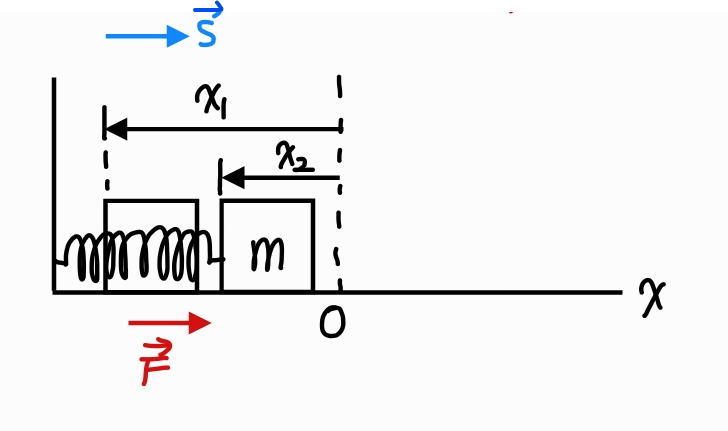
x₁과 x₂ 모두 음의 부호를 가지는데, x₂가 x₁보다 큰 값을 가진다.

따라서 용수철은 풀리면서 양의 일을 하게 되고 물체의 속도를 증가시킨다.

 

중력에 의한 일에서와 같이 용수철이 한 일을 두 지점에서 어떤 한 양의 차로 나타낼 수 있다. 따라서, 탄성 위치 에너지(elastic potential energy)를 다음과 같이 정의한다.

 

 

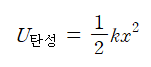
위 식을 사용하여 변형된 용수철의 힘에 의한 일을 위치 에너지의 변화로 나타낼 수 있다.

 

 

 

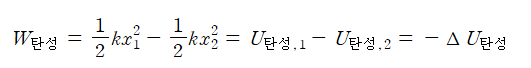
이로부터 용수철은 늘어나거나 압축될수록 탄성 위치 에너지가 증가한다는 사실을 알 수 있다.

 

 

 

 

 

 

참고문헌 : Young and Freedman, 대학물리학 12th ed, Haliday 일반 물리학 9th ed