[고전역학 | Mechanics] 10. 회전운동

# 회전운동학

회전운동을 분석하기 위해 고정된 한 축을 중심으로 회전하는 강체를 가정한다.

강체란 구성요소가 고정되어 있어서 모양이 변하지 않으면서 회전할 수 있는 물체를 말한다.

 

 

위 그림에서 각 위치 θ는 x축의 양의 방향에 대해 측정한 각도이며, 라디안(radian)을 사용하여 나타낸다.

라디안의 단위로 표현한 θ는 호의 길이 s를 반지름 r로 나눈 것과 같다.

 

라디안으로 표현된 각도는 두 길이의 비율이므로, 차원이 없는 순수한 숫자이다.

 

 

 

 

위 그림처럼 각 위치가 θ₂에서 θ₁으로 변할 때의 각도의 차이 ⧍θ를 각변위라 하고, ⧍θ=θ₂-θ₁로 표기한다.

이러한 각변위는 강체를 구성하는 모든 입자에 대해서 성립한다.

따라서 각변위는 반시계 방향으로 운동할 때 양의 값을 가지며, 시계방향으로 운동할 때 음의 값을 갖는다.

 

또한 시간 간격 ⧍t=t₂-t₁ 동안 회전체가 θ₂에서 θ₁으로 운동하는 경우, 평균 각속도(average angular velocity)는 다음과 같이 정의한다.

 

 

 

시간 ⧍t가 0으로 접근하는 경우의 순간 각속도(instantaneous angular velocity)는 t에 대한 θ의 미분 도함수로서 다음과 같이 정의한다.

 

 

 

주어진 시간 동안 회전하는 강체 위에 여러 점은 그 점이 회전축으로부터 얼마나 떨어져 있느냐에 따라 각각 다른 이동 거리를 움직인다. 그러나 물체는 강체이므로 같은 시간 동안 강체의 모든 점은 같은 속도로 회전한다.

따라서 어느 순간에서나 회전하는 강체의 모든 부분은 같은 각속도를 갖는다. 각속도의 단위는 초당 라디안(rad/s)을 사용하며, 분당 회전수(rev/min, rpm)와 같은 다른 단위들도 종종 사용한다.

 

 

 

시간 간격 ⧍t 동안의 각속도의 변화량을 각가속도라 한다. 회전체의 평균 각가속도(average angular acceleration)는 다음과 같이 정의한다.

 

 

 

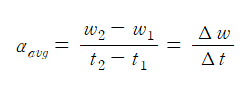
시간 ⧍t가 0으로 접근하는 경우의 순간 각가속도(instantaneous angular acceleration)는 t에 대한 θ의 미분 도함수로서 다음과 같이 정의한다.

 

 

각가속도는 제곱 초당 라디안(rad/s²)또는 제곱 초당 회전수(rev/s²)의 단위를 사용한다.

또한 w=dθ/dt이므로 각가속도는 각 좌표의 2차 도함수로 표현할 수 있다.

 

 

 

 

 

 

각가속도는 벡터량으로 방향을 갖는 값이다. 각가속도의 방향은 오른손 규칙을 이용하여 정의한다.

 

 

 

 

 

그러나 회전운동 시, 각변위는 벡터로 다룰 수 없다는 점을 유의하여야 한다.

벡터의 경우 합의 교환법칙이 성립하여야 하는데 각변위는 합의 교환법칙이 성립하지 않으며,

순서에 따라 각변위가 다른 값을 갖기 때문에 각변위는 벡터가 될 수 없다.

 

 

 

 

 

 

 

 

이때, 등가속도 직선운동과 같이 각가속도가 일정한 경우의 회전운동을 생각해본다.

 

w₀를 t=0일 때의 강체의 초기 각속도라 하면, 0부터 t까지의 시간 간격에 대해서 각속도 w는 w = w₀+αt와 같이 나타낼 수 있다. 일정한 각가속도 하에서 각속도는 일정 비율로 증가하므로, 0과 t사이의 평균 각속도는 초기 각속도와 나중 각속도의 산술 평균값과도 같다.

 

 

또한, 평균 각속도는 총 각변위를 시간 간격으로 나눈 값이므로 위 식을 다음과 같이 쓸 수 있다.

 

 

 

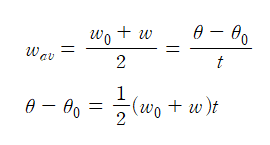
여기에 w = w₀+αt를 대입하면,

 

 

따라서

 

 

 

 

이다. 등가속도운동에서와 마찬가지로 위 운동방정식을 t에 대해 소거하면 다음과 같은 식을 얻는다.

 

 

 

 

 

 

 

병진운동과 회전운동의 운동 방정식을 비교한다.

 

 

                            <병진운동>                                         <회전운동>

 

 

 

 

 

 

 

 

 

 

# 선운동과 회전운동의 관계

강체가 고정된 한 축을 중심으로 회전할 때, 강체 내 모든 입자는 원 궤도를 따라 운동한다.

 

 

 

 

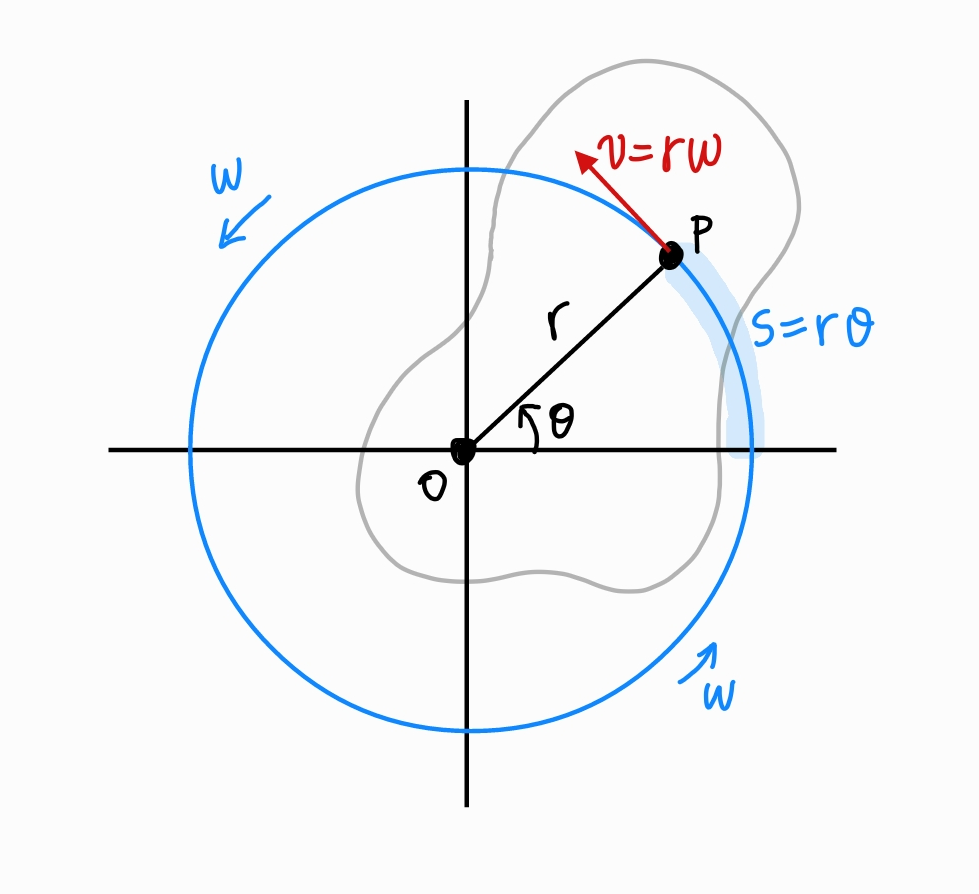
강체의 경우 모든 입자의 각속력 w는 같은 값을 갖지만, 축에서 멀리 떨어진 입자일수록 이동 거리는 더 큰 값을 갖는다.

 

따라서 강체의 기준선이 각도 θ만큼 회전할 때, 회전축에서 r만큼 떨어진 입자는 원호의 길이 s만큼 이동한다.

이때, 라디안 정의식으로부터 s=rθ로 나타낼 수 있으며, 각 θ는 라디안 값을 사용하여야 한다.

 

강체가 회전하는 동안 반지름 r은 일정하다고 가정하고, s=rθ의 양변을 시간에 대해 미분한 다음 절댓값을 취한다.

 

위 식의 좌변은 호의 길이 변화율로 입자의 순간 선속력 값을 의미하며, 위 식의 우변은 반지름과 각 변화율의 절댓값 곧, 순간 각속력의 크기를 의미한다.

 

따라서,

 

v=rw

 

이다. 이때 w는 반드시 rad 단위로 나타내야 한다.

 

위 식으로부터 축에서 거리가 멀수록 입자의 선속력은 증가하며, 입자의 선속도 벡터의 방향은 각 점에서 그 입자의 원형 경로에 접선 방향임을 알 수 있다. 강체의 각속력 w가 일정하다면, v=rw에 따라 v도 일정한 값을 갖는다. 따라서 강체 내의 모든 입자는 등속원운동을 한다.

 

 

입자가 경로를 따라 한 바퀴 회전하는 데 걸리는 시간 T는 다음과 같이 구할 수 있다.

 

 

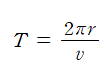
위 식에 v=rw를 대입하면,

 

 

와 같이 나타낼 수 있다.

즉, 한 바퀴 회전하는 데 걸리는 시간은 1회전에 해당하는 각변위 2π를 각속력으로 나눈 값과 같다.

 

다음으로 원 궤도를 운동하는 입자는 구심 가속도와 접선 가속도로 나타낼 수 있으므로, 이를 수식으로 나타내본다.

순간속도와 평행한 성분은 가속도의 접선 성분(tangential component of acceleration)이라 하며, v=rw의 식에 도함수를 취하여 얻을 수 있다.

곧,

 

 

이다. 접선 가속도 역시 rad 단위로 나타내어야 한다.

입자가 원 운동하기 위해서, 입자의 선가속도에는 원의 중심 방향을 향하는 구심 가속도(centripetal component of acceleration)가 존재해야 한다. 구심 가속도 식 a=v²/r 로부터 다음과 같이 나타낼 수 있다.

 

 

이 식은 w와 v가 일정하지 않은 경우에도 성립하며, 구심 가속도의 방향은 항상 회전축 방향으로 향한다.

 

회전하는 물체 내에 있는 입자의 선 가속도는 가속도의 구심 성분과 접선 성분의 벡터합이다.

 

 

 

 

 

 

 

 

 

 

 

 

 

# 회전운동의 에너지

회전하는 강체 내부에 서로 다른 선속력으로 움직이는 입자가 있을 때, 이들 각각의 운동 에너지를 합하여 물체 전체의 운동 에너지를 구할 수 있다.

즉,

 

 

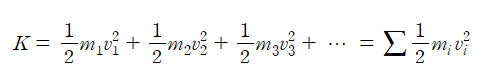
이다. 위 식에 v=wr을 대입하면,

 

 

 

이다. 여기서 회전하는 물체는 강체이므로 w는 모든 입자에 대해 같은 값을 갖는다.

위 식의 괄호 속의 기호는 회전체의 질량이 회전축에 대해 어떻게 분포하는지 나타내는 값이다.

이를 특정한 회전축에 대한 물체의 회전관성(rotational inertia) 또는 관성모멘트(moment of inertia) I라고 한다.

특정한 회전축에 대해서 강체의 회전관성은 일정한 값을 갖는다.

 

따라서 회전관성은 다음과 같이 정의한다.

 

 

회전관성 I의 SI 단위로는 kg⦁m²을 사용한다.

이를 위의 운동 에너지 식에 대입하여 강체의 회전 운동 에너지(rotational kinetic energy)를 나타낼 수 있다.

 

 

이 식을 유도하는데 v=wr를 사용하였으므로 w는 rad 단위를 사용하여야 한다.

 

 

다음으로, 각기 다른 위치에 있는 여러 입자에 대한 중력 위치 에너지를 생각해본다.

 

 

위 식은 질량 중심의 정의로부터 다음과 같이 나타낼 수 있다.

 

 

여기에서 M은 입자의 총질량을 말하며 중력 가속도 g가 모든 입자에 대해 같은 값을 가질 때, 중력 위치 에너지는 마치 물체의 질량 중심에 모든 질량이 집중되어 해당 중심점에서 중력만이 작용하는 경우와 같다.

 

 

따라서, 중력 위치 에너지 U는

 

 

이다.

 

 

 

 

 

 

 

이번에는 물체를 몇 개의 입자가 아닌, 물질이 연속적으로 분포할 때의 회전관성을 계산한다.

 

물체 내에서 모든 점의 밀도는 같은 값을 가질 때, 시그마 합을 적분으로 바꾸어 물체의 회전관성을 나타낼 수 있다.

물체를 충분히 작은 질량 요소 dm으로 나누어 각 요소 내의 모든 점이 회전축과 거의 동일한 수직 거리에 있다고 할 때, 이 거리를 r이라 하면

 

 

이다. 가느다란 막대와 같은 1차원 물체의 경우, 길이 방향으로 좌표 x를 설정하고 dm을 길이 요소 dx와 관련시킨다.

3차원 물체의 경우 dm을 부피 요소 dV와 물체의 밀도 ρ로 표현한다. ρ=dm/dV이므로,

 

 

 

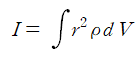
이다.

 

또한, 부피 요소 dV를 dxdydz와 같이 적분 변수의 미분항으로 표현하여 계산할 수 있다.

 

 

 

관성모멘트 계산 시, 주어진 축에서의 회전관성을 알고 있다면 주어진 축과 평행이면서 물체의 질량 중심을 지나는 새로운 축에 대해서 회전관성을 구할 수 있다.

주어진 축과 질량 중심을 지나는 축과의 수직 거리를 h라 할 때, 새로운 축에 대한 회전관성은 다음과 같이 구할 수 있다.

 

 

임의의 모양인 물체의 단면에서 O는 물체의 질량 중심을 의미한다.

O를 지나는 축에서 계산한 물체의 회전관성을 I‘이라 할 때, 점 P(a,b)를 지나면서 O를 지나는 축과 평행한 새로운 평행 축에서의 회전관성은 다음과 같다.

 

 

첫 번째 항은 O을 지나는 평행축에서의 회전관성 값을 의미한다.

질량 중심의 정의에 따라 두 번째 항과 세 번째 항은 각각 물체의 x, y 질량 중심 좌표를 의미한다. 즉, 0이 되어 사라진다.

마지막 항은, 점 O부터 점 P까지의 거리를 의미하며 h로 나타낸다.

 

따라서 식은

 

 

이다. 이 식을 평행축 정리라 한다.

 

 

 

 

 

 

 

 

 

 

 

 

 

# 관성모멘트 계산

위에서 관성모멘트에 대해 정의한 식을 바탕으로 다양한 물체의 관성 모멘트를 직접 계산해본다.

관성모멘트 계산 시 미소요소를 가정할 때, 항상 그 안의 모든 점은 회전축과 거의 같은 거리에 있도록 해야 한다.

 

먼저 질량 M, 길이 L의 균일하고 가느다란 막대를 가정한다. 한쪽 끝에서 임의의 거리 h만큼 떨어진 점 O를 지나는 축에 대한 관성 모멘트를 계산한다.

 

 

전체 질량 M에 대한 질량소 dm의 비율은 전체 길이 L에 대한 길이 dx의 비율과 같다.

따라서

 

이다. 이를 이용하여 관성모멘트를 나타내면

 

 

와 같이 나타낼 수 있다.

 

축이 오른쪽 끝에 있는 경우, h=0이고 관성모멘트 값은

 

 

이다.

 

 

축이 왼쪽 끝에 있는 경우, h=L이고 관성모멘트 값은

 

 

이다.

 

 

 

축이 막대 중심을 지나는 경우, h=L/2이고 관성모멘트 값은

 

 

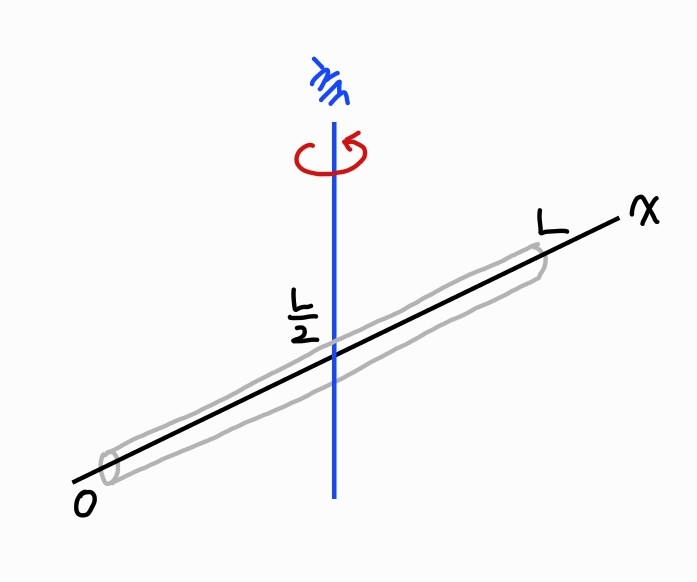
이다.

 

 

 

 

 

 

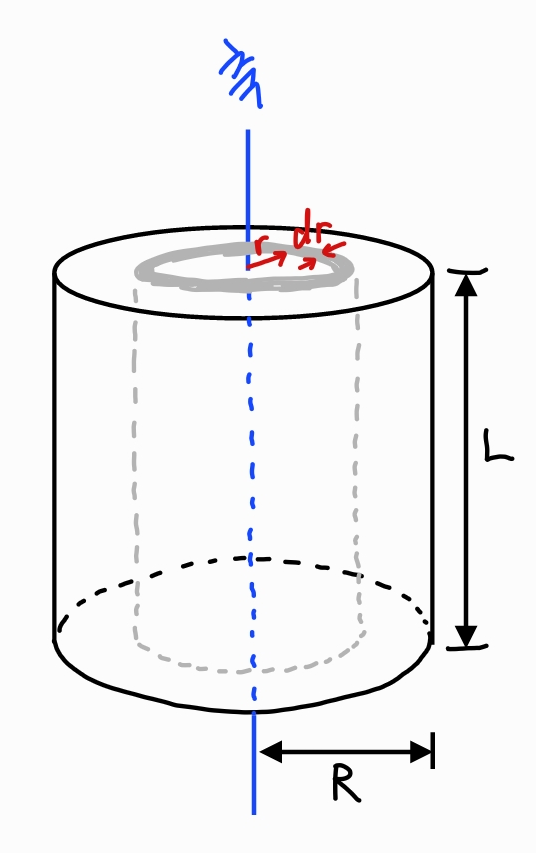
다음으로 속이 빈 원통의 관성모멘트를 계산한다.

 

 

원통의 부피요소로서 반지름 r, 두께 dr, 길이 L의 얇은 원통 껍질을 가정한다.

그러면 이 얇은 원통은 평평한 판으로 가정하여 미소 부피를 구할 수 있다.

 

dm=ρdV=ρ(2πrLdr)

 

이를 활용하여 속이 빈 원통의 관성모멘트를 구한다.

 

 

이때 위 원통의 부피는

 

이고, 원통의 질량은 부피에 밀도를 곱한 값이므로

 

 

와 같이 나타낼 수 있다.

 

따라서 관성 모멘트를 원통의 질량으로 간단히 표현하면

 

이다.

 

 

만약 원통의 속이 가득 차있는 경우, R₁은 0이다.

바깥쪽 반지름 R₂를 그냥 R로 나타내면, 반지름이 R인 속이 찬 원통의 관성 모멘트는 

 

 

 

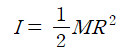
이다.

 

 

 

원통이 매우 얇은 두께를 갖는 경우, 바깥쪽 반지름과 안쪽 반지름은 거의 같은 값을 갖게 되어 R₁=R₂=R과 같이 공통의 반지름으로 나타낼 수 있다. 즉, 매우 얇은 원통의 관성모멘트는

 

 

 

이다.

 

 

 

 

 

 

다음으로 직사각형 판의 관성모멘트를 계산한다.

질량이 M인 직사각형 판의 회전축이 판의 중심을 지나는 경우의 관성모멘트는

 

이고, 직사각형 판의 회색으로 표시한 사각형의 미소면적 dm은 dm=ρdxdy와 같이 나타낼 수 있다.

따라서

 

 

 

이다. 이때, 직사각형의 넓이는 ab이므로, 질량은 ρab와 같이 나타낼 수 있다.

즉, 관성모멘트를 질량을 활용하여 간단하게 나타내면

 

 

 

 

이다.

 

 

이번에는 위의 직사각형 판에서 회전축이 직사각형 판의 가장자리를 지나는 경우,

 

 

 

직사각형 미소요소 dm=ρbdx이므로, 

 

 

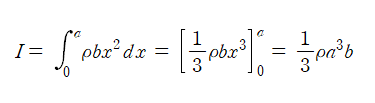
이다. 이때, 직사각형의 넓이는 ab이므로 질량은 ρab와 같이 나타낼수 있다.

즉, 관성모멘트 식을 질량을 활용하여 간단하게 나타내면

 

 

이다.

 

 

 

 

 

 

 

다음으로 질량 M, 반지름 R인 원판의 관성모멘트를 계산한다.

 

 

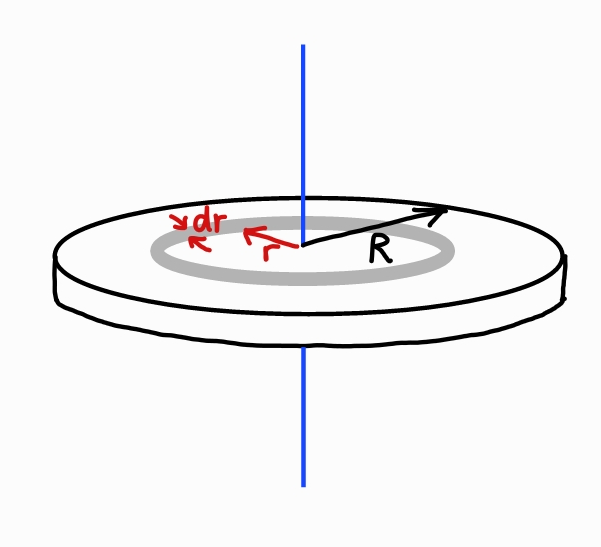
미소면적으로 회색으로 색칠한 얇은 고리를 가정한다. 이 얇은 고리를 펼쳤다고 가정하고 펼친 고리의 직사각형의 넓이와 미소 면적은 같은 값을 갖는다. 펼친 고리는 너비 2πr, 높이 dr의 직사각형이므로 미소면적은 dm=2ρπrdr 와 같이 나타낼 수 있다. 

 

따라서 관성모멘트 값을 계산하면

 

 

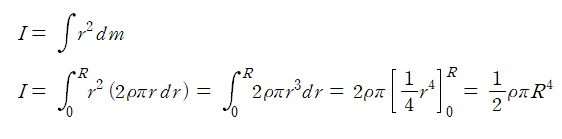이다. 이때 원판의 넓이는 πR²이므로 원판의 질량은 ρπR² 이다.

관성모멘트 식을 질량을 활용하여 나타내면

 

 

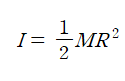이다.

 

 

 

 

 

그렇다면 질량 M, 내부 반지름 R₂, 외부 반지름 R₁ 인 원형 고리를 가정한다.

이 고리의 관성모멘트는 위에서 구한 원판의 관성모멘트 식에서 적분 범위를 0부터 R이 아닌 R₂부터 R₁까지 계산한 값과 같다.

 

 

 

원판의 넓이는

 

 

 

이므로 질량은

 

 

 

 

관성모멘트 식을 질량을 활용하여 나타내면

 

 

이다.

 

 

 

 

 

 

 

 

마지막으로, 구에 대해서 관성모멘트를 구한다.

 

속이 비어 있지 않은 반지름이 R, 질량 M인 구를 가정하고, 구의 관성모멘트는 구를 이루는 미소원판들의 관성모멘트의 합으로 나타낼 수 있다.

 

 

 

미소원판의 관성모멘트 dI를 모두 합하여 구의 관성모멘트 I를 구하고자 한다.

원판의 관성모멘트는 앞에서 유도하였던 식과 같이 dI=(1/2)r²dm 으로 나타낼 수 있다.

 

 

 

이때, 미소원판의 질량 dm은 dm=ρπr²dz와 같이 나타낼 수 있으며 직각삼각형의 성질에 따라 r²+z²=R², r²=R²-z² 의 관계식을 유도할 수 있다. 이를, 대입하여 나타내면

 

dm=ρπ(R²-z²)dz

 

 

 

 즉,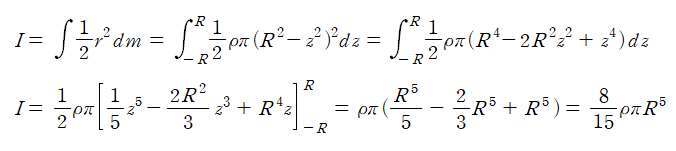

 

 

 

이다. 

이때, 구의 부피는

 

 

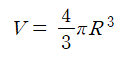
이므로, 질량은 

 

와 같이 나타낼 수 있으며, 구의 관성모멘트를 질량을 활용하여 간단히 나타내면

 

 

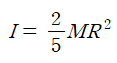
이다.

 

 

 

다음은 속이 비어 있지 않은 구의 관성모멘트를 유도할 때, 발생하는 실수에 관한 틀린 풀이이다.

 

구 내부의 작은 구 껍질을 가정한다. 구 껍질의 미소면적 dm는 구의 겉넓이 식을 활용하여 나타낸다.

dm=ρdV=ρ(4πr²dr)

 

따라서

 

이고, 구의 질량으로 간단히 나타내면 

 

 

와 같은 식을 얻을 수 있는데 이는 틀린 풀이이다.

왜냐하면 회전축으로 물체가 회전하는 것이 아닌, 구의 중심으로 물체가 회전한다고 가정하여 관성모멘트를 구한 것이기 때문이다. 즉, 구의 중심으로부터의 거리 r을 가정하는 것이 아니라 회전축으로부터의 거리 r을 고려해야한다.

 

 

 

 

 

 

이번에는 구의 속이 비어있다고 가정하여 관성모멘트를 구한다. 

질량 M, 반지름 R의 위와 같은 구를 가정한다.

 

 

속이 빈 경우 원형 고리의 관성모멘트 dI의 합으로 표현한다.

원형 고리의 관성모멘트는 앞에서 유도했던 것과 같이 dI=(1/2)(R₁²+R₂²)dm이며, 얇은 껍질일 경우 두 반지름은 반지름 R로 근사한다. 즉, dI=R²dm 이다.

 

 

 

 

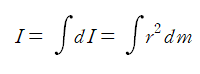
이때 원형고리의 미소 질량 dm은 dm=2ρπrdz 와 같이 나타내고자 한다. 그러나 이러한 값은 구의 겉넓이를 정확하게 반영하지 못하므로 틀린 값이 나오게 된다.

 

 

즉, 미소 질량을 다음과 같이 정의한다.

 

 

dm=2ρπrRdθ

 

이를 대입하여 관성모멘트를 계산한다.

 

 

 

위 적분을 계산하기 위해 θ를 z에 대한 식으로 치환한다. z=Rsinθ, dz=Rcosθdθ 

또한 원형고리의 반지름을 각 θ를 활용하여 표현하면 r=Rcosθ이다.

 

따라서

 

 

 

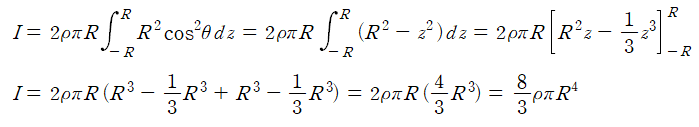이때 구껍질의 겉넓이는 4πR² 이므로 질량은 4ρπR² 이다. 

관성모멘트를 질량을 활용하여 간단하게 나타내면

 

 

이다.

 

 

 

 

 

 

 

 

 

 

 

 

 

참고문헌 : Young and Freedman, 대학물리학 12th ed, Haliday 일반 물리학 9th ed