[고전역학 | Mechanics] 12. 평형과 탄성

# 평형

어떤 물체가 평형 상태가 되기 위한 조건은 다음과 같다.

 

 

 

이때 물체는 정적 평형(static equilibrium)상태에 있다고 한다.

물체가 힘을 받아 움직였다가 다시 정적 평형으로 되돌아오면 물체는 안정한 평형상태에 있다고 한다. 한편 작은 힘으로도 물체를 움직여 평형상태에서 벗어나게 할 수 있을 경우 물체가 불안정한 평형상태에 있다고 한다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 평형 조건

물체의 병진운동은 뉴턴의 제 2법칙인 다음의 식을 만족한다.

 

 

만약 물체가 병진운동에 대해 평형상태에 있으면 운동량은 상수값을 가지므로,

 

 

이다. 즉,

 

 

 

 

입자에 작용하는 힘의 벡터합이 0인 경우, 그 입자는 가속되지 않으므로 관성 기준계에서 평형 상태에 있다.

이를 평형 제 1조건(first condition for equilibrium)이라고 한다.

 

 

 

여기서 힘은 외력에만 해당한다.

 

 

두 번째로, 물체의 회전운동은 각운동량에 대한 뉴턴의 제 2법칙인 다음의 식을 따른다.

 

 

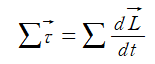
만약 물체가 회전운동에 대해 평형상태에 있다면 각운동량은 상수값을 가지므로,

 

 

 

이다. 즉,

 

 

 

따라서 물체에 작용하는 모든 외력에 의한 돌림힘의 합이 0이어야 하며, 평형 상태에 있는 강체는 어느 점에 대해서도 회전하려는 경향이 없어야 한다. 이를 평형 제 2조건(second condition for equilibrium)이라고 한다.

 

 

 

 

정지한 상태의 물체에 대해서 1조건과 2조건을 만족할 때, 이 물체는 평형상태에 있다고 한다. 그러나 해당 평형은 정적 평형상태는 아니며, 정적 평형상태에 있기 위해서는 선운동량 P가 0이 되어야 한다.

 

따라서 정적 평형 상태가 되기 위한 또 하나의 조건은 다음과 같다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 무게 중심

물체에 작용하는 중력은 물체의 각 부분에 작용하는 중력의 벡터합이다. 이는 물체의 무게중심(center of gravity, cog)이라고 하는 하나의 점에 작용하는 것으로 간단히 나타낼 수 있다.

 

물체의 모든 부분에 대해서 같은 중력가속도가 작용한다면, 물체의 질량중심(center of mass)과 무게중심(cog)은 일치한다.

 

이를 증명하기 위해 질량 M으로 이루어진 물체를 가정한다.

 

 

 

물체의 각 미소요소의 질량은

 

이므로 각 요소마다

 

 

의 중력이 작용한다.

 

미소요소의 각각의 중력으로 인해 물체는 원점 O에 대해서

 

 

의 토크를 만들게 된다.

따라서 물체의 모든 부분에 작용하는 알짜 토크는 다음과 같다.

 

 

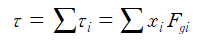
다음으로 전체 물체에 대해서 살펴본다.

 

 

전체 물체에서 물체의 무게중심에 작용하는 중력은 위 그림과 같이 나타난다.

이 힘은 원점 O에 대해

 

 

의 토크를 발생시킨다.

 

한편 물체의 무게중심에 작용하는 중력은 각 부분에 작용하는 중력의 벡터 합과 같으므로

다음과 같이 표기할 수 있다.

 

 

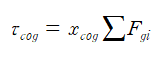
또한 무게중심에 작용하는 중력이 만드는 토크는 물체의 미소 요소에 작용하는 중력이 만드는 토크의 합과 같으므로

 

 

와 같이 나타낼 수 있다. F=mg이므로

 

 

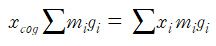
이때 물체 내 모든 지점에서 중력 가속도가 같은 값을 갖는다면, 양 변을 약분할 수 있다.

 

 

또한 모든 미소요소의 질량 합은 물체의 전체 질량 M이므로

 

 

이다. 이때, 위 식의 우변은 물체의 질량중심 x좌표를 의미하므로

 

 

이다. 따라서 중력가속도가 같은 값을 가질 때, 질량중심과 무게중심은 일치한다.

 

질량 중심은 다음과 같이 정의할 수 있다.

 

 

 

질량 중심의 x,y,z 값은 위치벡터의 성분으로 활용할 수 있으므로, 다음의 벡터 방정식으로 나타낼 수 있다.

 

 

 

어떤 물체의 무게 중심을 찾고자 할 때, 질량 중심을 찾는 경우와 마찬가지로 대칭관계를 이요할 수 있다.

 

균일한 구, 정육면체, 원형 또는 직사각형 판 등의 무게 중심은 기하학적인 중심에 있다.

원통이나 원뿔 모양의 물체들의 무게 중심은 대칭축 위에 있다.

 

만약 더 복잡한 형태의 물체의 경우, 대칭성을 가진 여러 물체로 나누어서 무게 중심을 구할 수 있다.

여러 물체들의 질량과 무게 중심 좌표를 나타내고, 이 물체들로부터 조합 전체의 무게중심을 질량중심 식을 이용하여 계산한다.

 

 

 

 

 

 

 

 

 

 

 

 

 

# 변형력, 변형, 탄성률

물체는 힘을 받으면 늘어나거나, 눌리거나 비틀리며 변형이 일어나게 된다. 이러한 힘과 변형사이의 관계를 나타내기 위해 변형력, 변형, 탄성률의 개념을 도입한다.

 

변형력(stress)이란 단위 면적당 작용한 힘을 말하며, 변형(strain)은 변형력이 작용하여 나타난 결과를 말한다. 이때, 변형력과 변형의 비를 탄성률(elastic modulus)이라 한다.

 

 

 

 

 

단면적 A가 균일하고 길이가 l₀인 물체에 인장력이 가해지는 경우를 생각한다.

 

 

단면에 작용하는 인장 변형력(tensile stress)는 힘과 단면적의 비로 정의한다.

 

 

 

이때 힘 F는 크기를 사용하므로 변형력은 스칼라량이다. 변형력의 SI단위로는 파스칼을 사용한다.

 

 

 

물체는 가해진 장력에 의해 길이가 l=l₀+⧍l로 늘어나며, 늘어난 길이 ⧍l는 막대의 모든 부분에서 똑같은 비율로 늘어나는 것이다.

 

 

 

물체의 인장 변형(tensile strain)은 늘어난 길이 ⧍l의 원래의 길이 l₀에 대한 비로 단위 길이당 늘어난 길이를 나타낸다.

 

 

인장 변형은 단위가 없는 순수한 수이다.

 

훅의 법칙으로부터 충분히 작은 인장 변형력이 작용하였을 때, 변형력과 변형은 비례관계에 있으므로 이러한 관계를 나타내기 위한 변형력과 변형의 비를 탄성률(Young’s modulus, Y)이라 한다.

 

 

 

 

 

 

 

다음으로 위와 같은 물체가 압축(compression)되는 경우를 생각한다.

 

 

물체가 압축될 때 받는 변형력을 압축 변형력(compressive stress)이라 하며, 원래 길이에 대한 줄어든 길이의 비를 압축 변형(compressive strain)이라 한다.

 

인장의 경우와 마찬가지로, 압축에 대해서도 변형력과 변형은 비례관계에 있다. 

 

 

 

대부분의 물질의 영률은 압축의 경우와 인장의 경우에서 같은 값을 갖는다.

 

 

 

 

 

 

 

 

한 면에 대해 힘이 작용하는 앞의 두 가지 경우와는 달리, 물체의 모든 면에 균일한 압력이 작용하는 경우 물체는 부피가 변화하게 된다. 

 

 

이때 이 힘은 물체의 표면에 수직으로 작용하며, 유체에 잠긴 물체의 표면에 유체가 단위 면적당 작용하는 힘을 유체 내에서의 압력(pressure, p)라고 한다.

 

 

압력은 변형력과 같은 SI단위를 사용한다.  또는 통상적으로 atm이라 표기하는 기압의 단위도 많이 사용한다.

1기압은 해수면에서의 지구 대기에 의한 근사적인 평균 압력을 말한다.

 

 

 

압력은 부피가 변할 때 물체에 변형력과 같은 역할을 한다.

물체에 가해진 압력이 p₀에서  p₀+⧍p로 변화할 때 이 변화량을 부피 변형력이라 한다.

 

 

물체에 압력 p를 가해 부피가 변화한다면 변한 부피 ⧍V와 초기 부피 V₀의 비율을 부피 변형이라고 한다.

 

 

 

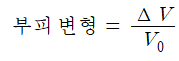
훅의 법칙에 의해 압력이 증가함에 따라 부피 변형은 이에 비례한다. 이러한 관계를 부피 탄성률(bulk modulus, B)로 나타낸다.

 

 

 

위 식에서 음의 부호는 압력이 증가함에 따라 부피가 감소하기 때문이며, 위 식의 부피 탄성률의 역수를 압축률(compressibility, k)이라 한다.

 

 

 

 

압축률은 압력의 단위 증가 ⧍p당 부피 감소 비를 나타낸다. 압축률의 단위는 압력의 역수이다.

 

 

 

 

 

마지막으로 크기는 같으나 방향이 반대인 두 힘이 물체에 작용하는 경우, 물체는 층밀리기 변형력(shear sress)을 받는다.

 

 

층밀리기 변형력은 표면에 대해 접선 방향으로 작용하는 힘을 표면의 넓이로 나눈 값으로 정의한다.

 

 

위의 그림과 같이 층밀리기 변형력을 받는 물체의 한쪽 면은 반대편 면에 대해서 거리 x만큼 밀린다. 층밀리기 변형(shear strain)은 변위 x와 높이 h의 비로 정의한다.

 

 

 

훅의 법칙에 의해 층밀리기 변형은 층밀리기 변형력과 비례관계이다. 이러한 관계를 층밀리기 탄성률(shear modulus, S)라 하고 다음과 같이 나타낸다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

# 탄성과 소성

물체에 힘을 가할 때, 변형력과 변형은 언제까지 서로 비례하는 값을 갖는지에 대해 알아본다.

 

 

물체에 계속해서 변형력을 가할 때, a점에 이르기까지 물체는 변형력이 변형에 정비례하는 훅의 법칙을 만족한다. 

이때, 점 a를 비례한계라고 부른다.

 

a부터 b까지는 변형력이 변형에 비례하지도 않고, 훅의 법칙을 만족하지도 않는다. 

 

그러나 b지점까지의 변형력을 가했을 때, 물체는 다시 원래의 길이로 되돌아 올 수 있으며 이때의 형태 변화는 가역적이다.

가해진 힘은 보존되며, 변형시키기 위해 투입된 에너지는 변형력이 제거되면 그대로 회수되며, 이 영역에서 물체는 탄성 거동을 보인다라고 한다. 이 영역의 끝인 점 b를 항복점이라고 하며 이 점에서의 변형력을 탄성 한계라고 한다.

 

b점 너머까지 변형력을 증가시키면, 변형력이 제거되더라도 금속은 원래 길이로 돌아오지 않으며, 물체는 빨간 선을 따라 변화한다. 이러한 경우 물체는 영구변형되었다라고 말한다.

 

c점을 넘어서 변형력을 증가시키면, 상대적으로 작은 변형력에도 큰 변형이 일어나다가 d점에 도달하면 물체에 균열이 발생하게 된다. 

 

 

점 b부터 점 d사이의 물체의 거동을 소성 흐름 또는 소성 변형이라 한다.

소성 변형은 비가역적이며 변형력을 제거하여도 원래 상태로 되돌아오지 않는다.

 

 

소성 변형이 잘 일어나는 물질은 연성이 크다고 하며, 탄성 한계를 지나자마자 곧 균열이 생기는 물질은 취성이 크다고 한다.

 

 

 

 

 

 

물체에 탄성한계 이내의 변형력을 가하더라도 변형력을 증가시킬 때와 감소시킬 때의 곡선이 다르게 나타나는 경우도 있다.

 

이와 같은 현상을 탄성 이력이라고 하며, 변형력을 감소시킬 때 증가시킬 때보다 적은 일을 필요로 한다.

이는 내부 마찰과 관계된 비보존력이 작용하기 때문이이다.

 

 

 

 

 

 

 

 

 

 

 

 

 

참고문헌 : Young and Freedman, 대학물리학 12th ed, Haliday 일반 물리학 9th ed