[고전역학 | Mechanics] 08. 에너지 보존

 

# 중력만 있을 때의 역학적 에너지 보존

물체에 무게만 작용한다고 가정했을 때, 이 물체가 공기저항을 받지 않고 자유낙하는 경우를 생각한다.

처음 위치와 속도를 각각 y₁, v₁, 나중 위치와 속도를 각각 y₂, v₂라 하자. 일-에너지 정리로부터 총 일은 W = ⧍K = K₂ - K₁임을 알 수 있으며, 중력이 그 물체가 받는 유일한 힘이므로, 총 일은 W = -⧍U = U₁ - U₂와 같이 나타낼 수 있다.

이 두 식으로부터 ⧍K = -⧍U임을 알 수 있으며, K₂ - K₁ = U₁ - U₂

즉, U₁ + K₁ = U₂ + K₂ 이므로

 

 

이다.

 

위 식으로부터 운동 에너지와 위치 에너지의 합 K + U를 계의 총 역학적 에너지(total mechanical energy of the system, E)라 부른다. 어떤 물체에 가해진 힘이 중력만 있다면, 총 역학적 에너지는 언제나 일정하다. 곧, 보존된다. 이는 역학적 에너지 보존 법칙(conservation of mechanical energy)이라고 한다.

 

물체의 역학적 에너지 보존 법칙이 성립할 때 작용하는 힘을 보존력이라 한다.  즉, 위의 경우에서 중력은 보존력이다.

 

 

 

 

낭떠러지에서 공을 떨어뜨렸을 때, 총 역학적 에너지는 운동 에너지와 중력 위치 에너지를 번갈아 가면서 전환되지만 두 에너지의 합은 항상 일정하다.

 

 

 

 

 

 

 

 

 

 

 

 

# 중력 외의 다른 힘들이 일을 하는 경우

무게 이외의 다른 힘이 물체에 작용하고 있는 경우, 전체의 일 W는 힘 F에 의한 일과 중력에 의한 일 W(중력)을 포함한다. 힘 F에 의해 발생한 일을 W(다른 힘)이라 하면, 전체 일은 W = W(중력) + W(다른 힘)와 같이 나타낼 수 있다.

따라서, 전체 일은 물체의 운동 에너지 변화량과 같으므로 W(중력) + W(다른 힘) = K₂ - K₁ 이다.

 

중력에 의한 일 W(중력)은 중력 위치 에너지의 정의에 의해 W(중력) = U₁(중력) - U₂(중력)이므로

W(다른 힘) + U₁(중력) - U₂(중력) = = K₂ - K₁ 이며, W(다른 힘) + U₁(중력) + K₁ = K₂ + U₂(중력) 이다.

즉,

 

 

이는 중력 이외의 다른 힘들이 한 일은 계의 총 역학적 에너지 E = K + U의 변화와 같음을 알 수 있다.

 

물체에 가한 힘 F에 의한 일 W(다른 힘)가 양의 값을 가지면, E는 증가하여 K₂ + U₂가 U₁ + K₁보다 크다. 반면 W가 음의 값을 가지면, E는 감소한다. 물체에 가해진 힘이 없는 경우 W(다른 힘)=0 이므로 총 역학적 에너지는 일정한 값을 갖게 된다.

 

 

 

더 나아가서 연직으로 내려진 용수철에 매달려 운동하는 물체를 생각해본다. 이러한 경우 물체에는 중력과 탄성력, 움직이는 물체에 대해 공기저항에 의한 힘이 작용한다. 이를 수식으로 표현하면, 일의 총 합은 중력이 한 일 W(중력), 탄성력이 한 일 W(탄성력), 그리고 다른 일이 한 일 W(다른 힘)의 합으로 나타낼 수 있다.

곧, W = W(중력) + W(탄성력) + W(다른 힘)이다.

 

그러면 일-에너지 정리에 의해, W(중력) + W(탄성력) + W(다른 힘) = K₂ - K₁이 된다.

중력이 한 일은 W(중력) = U₁(중력) - U₂(중력)이고, 용수철에 의한 일은 W(탄성력) = U₁(탄성력) - U₂(탄성력) 이므로,

U₁(중력) - U₂(중력) + U₁(탄성력) - U₂(탄성력) + W(다른 힘) = K₂ - K₁ 가 되며,

 

K₁ + U₁ + W(다른 힘) = K₂ + U₂ (U₁ = U₁(중력) + U₁(탄성력), U₂ = U₂(중력) + U₂(탄성력)) 와 같이 나타낼 수 있다.

 

이렇게 중력 위치 에너지와 탄성 위치 에너지의 합으로 나타낸 U₁, U₂를 간단히 위치 에너지라고 부른다.

 

 

 

 

 

 

 

 

 

 

# 보존력과 비보존력

운동 에너지와 위치 에너지 간에 양방향 변환이 가능한 경우, 즉 W₁ = -W₂일 때, 작용하는 힘을 보존력(conservative force)이라 한다. 보존력에는 중력과 용수철 힘과 같은 것들이 있다. 보존력은 해당 힘이 한 일은 경로에 무관한 성질을 가지며(가역적), 초기위치와 최종위치에 의해서만 결정된다. 즉, 일은 위치 에너지 함수의 처음 값과 나중 값의 차이로 표현할 수 있으며, 출발점과 도착점이 같은 경우에 전체 일은 0의 값을 갖게 된다.

물체에 가해진 모든 일이 보존력에 의한 것이라면, 총 역학적 에너지 E = K + U는 항상 보존된다.

 

 

다음은 보존력은 경로에 무관하다는 성질을 증명해본다.

 

 

 

입자가 경로 1을 따라 초기위치 a에서 b로 움직인 다음, 경로 2를 통하여 점 a로 되돌아오는 왕복운동을 가정한다.

이때 각각의 경로에서 입자의 움직임에 따른 일을 가하게 된다.

 

a에서 b까지 경로 1을 따라 한 일을 W(ab,₁), b에서 a까지 경로 2를 따라 한 일을 W(ba,₂)로 표기한다.

만일 힘이 보존력인 경우 왕복운동을 하는 동안에 한 알짜 일은 0이 되므로, W(ab,₁) + W(ba, ₂) = 0, W(ab,₁) = -W(ba,₂)이다.

 

 

다음으로 입자가 경로 2를 따라 a에서 b로 운동할 때 입자에 가한 일 W(ab,₂)을 고려한다.

만일 힘이 보존력이라면 W(ab,₂)은 위에서 구한 W(ba,₂)의 음의 값과 같다. 즉, W(ab,₂) = -W(ba,₂)이므로 이를 W(ab,₁) = -W(ba,₂)에 대입하면, W(ab,₁) = W(ab,₂)이므로 보존력은 경로에 무관하다는 것을 알 수 있다.

 

 

한편 보존되지 않는 힘은 비보존력(nonconservative force)이라 한다. 비보존력에는 마찰력과 항력과 같은 힘이 있으며, 이러한 힘들은 위치 에너지 함수로 표현할 수 없다. 비보존력이 물체에 가해지면, 이러한 힘들은 역학적 에너지의 손실을 일으키거나 분산시켜 버린다. 혹은 역학적 에너지를 증가시키기도 하며, 이러한 반응들은 모두 비가역적이라는 성질을 갖고 있다.

 

비보존력은 위치 에너지의 함수로 나타낼 수 없으나, 내부 에너지(internal energy)를 이용하여 표현할 수 있다.

물체의 내부 에너지는 물질 상태 변화와 관련된 에너지로서, 물체의 온도를 높이면 내부 에너지가 증가하고, 온도를 낮추면 내부 에너지는 감소하게 된다.

실험을 통해 내부 에너지의 증가는 마찰력이 한 일의 절댓값과 일치한다는 사실을 알 수 있다.

 

즉, ⧍U = -W(다른 힘) 이며 위의 K₁ + U₁ + W(다른 힘) = K₂ + U₂의 식에 대입하면,

K₁ + U₁ - ⧍U = K₂ + U₂을 얻는다.

⧍K = K₂ - K₁, ⧍U = U₂ - U₁ 라 하면,

 

 

와 같이 나타낼 수 있으며, 위 식을 일반적 형태의 에너지 보존 법칙이라고 한다.

어떠한 과정에서 운동 에너지, 위치 에너지, 그리고 내부 에너지는 모두 변할 수 있으나 이 변화량의 합은 항상 0이다.

한 형태의 에너지가 감소하면 다른 형태의 에너지가 증가함으로 감소량을 보충하게 된다. 따라서, 에너지는 만들어지거나 소멸하지 않으며 다른 형태로 변환되는 것임을 알 수 있다.

 

 

 

 

 

 

 

 

 

# 에너지 도표

위치 에너지에 대해 보존력이 어떠한 역할을 하는가에 대해 알아본다.

보존력에 의한 일 W는 위치 에너지 변화 ⧍U의 음의 값에 해당하므로, W = -⧍U이다. 입자가 1차원 공간에서 미소 변위 ⧍x만큼 움직일 때, 입자에 작용하는 힘이 한 일 W는 입자에 작용하는 힘 F와 ⧍x의 곱과 같다.

즉, W = -⧍U(x) = F(x)⧍x이며, F(x) = -⧍U(x)/⧍x와 같이 나타낼 수 있다.

우변의 미소 변위 ⧍x을 0으로 근사하게 되면

 

 

이다.

 

이번에는 입자를 3차원 공간으로 확장하여 생각해본다.

입자에 가해지는 힘은 각각 x, y, z의 함수이며, 위치 에너지도 x, y, z의 함수로서 U(x, y, z)로 표현할 수 있다.

 

1차원 공간에서 x축 방향에 대한 F(x) = -⧍U(x)/⧍x의 식을 활용해 3차원 공간상에서의 각 성분의 값을 각각 구할 수 있다.

x축 방향의 작은 변위 ⧍x에 대한 위치 에너지 변화 ⧍U는 -Fₓ⧍x이다. 이때, F의 y성분과 z성분은 ⧍x와 수직이므로 일을 하지 않는다. 따라서 근사식

 

 

을 얻는다. y-성분과 z-성분에 대해서도 마찬가지로

 

 

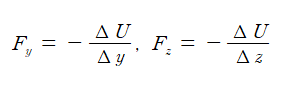
의 값을 얻을 수 있다.

이때, 각각의 미소 변위를 0으로 근사하게 되면 다음과 같은 식을 얻을 수 있다.

 

 

이러한 도함수를 편도함수를 이용하여 벡터식으로 표현하면 다음과 같다.

 

 

따라서, 힘 F는 U를 각 좌표로 편미분을 한 다음, 그 좌표에 해당하는 단위 벡터를 곱한 후 벡터합을 취하여 구할 수 있다. 이를 U의 기울기 벡터(gradient)라고 하며, 간단히 ∇기호를 사용하여 나타낸다.

 

 

 

 

 

 

 

x의 함수로 나타낸 E의 그래프를 에너지 도표(energy diagram)라고 한다.

이 도표는 위치 에너지 함수 U와 U에 의한 힘을 받고 움직이는 입자의 에너지도 함께 나타낸다.

다음은 일반적인 위치 에너지 함수의 그래프와 이 곡선에 대한 힘의 그림이다.

 

 

 

물체에 가해진 힘이 보존력일 때, 총 에너지 E = K + U는 항상 일정한 값을 갖는다. 그러므로 각 점에서 U와 E사이의 수직 거리 E – U는 그 점에서의 운동 에너지 K에 해당한다. K의 값이 가장 큰 지점에서 물체는 최대 속력을 갖게 되며, 위치 에너지는 총 에너지 E를 능가할 수 없다.

 

각 점에서 물체에 작용하는 힘 F는 U곡선의 기울기에 음의 부호를 붙인 것과 같다.

 

 

위치 에너지의 기울기가 0일 때, 이 지점은 평형(equilibrium)의 위치이다. 일반적으로 위치 에너지 곡선에서 극소점은 안정 평형점(stable equilibrium)이라 하며, 극대점은 불안정 평형점(unstable equilibrium)이라 한다.

위 그래프에서 x1과 x3은 안정 평형점이다. 이 두 점에서는 U(x)곡선의 기울기가 0이므로, 힘 F도 0의 값을 갖는다. 입자가 바깥쪽으로 이동하는 경우, 힘이 작용하여 입자를 평형점으로 끌어들이다. 

x2, x4 점들은 불안정 평형점이며, 입자가 약간 오른쪽이나 왼쪽으로 이동하는 경우 U곡선의 기울기는 음의 값을 갖고, 힘 F는 양의 값을 가지므로 입자를 더욱 멀리 밀어내게 된다. 

 

총 에너지가 E1이며, 처음에 입자가 x1부근에 있다면, 물체는 E1과 U가 만나는 점 xa와 xb사이에서만 움직이게 된다. 이러한 입자의 운동을 퍼텐셜 우물 속의 운동이라고 하며, xa와 xb는 입자 운동의 회귀점이라고 한다. 총 에너지를 E2까지 증가시키면 입자는 더욱 넓은 영역인 xc, xd사이를 움직인다. 총 에너지가 E3이상이 되면, 입자는 x의 무한대까지 탈출할 수 있다. 또한 E0는 이 계에서 가질 수 있는 최소의 에너지이다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

참고문헌 : Young and Freedman, 대학물리학 12th ed, Haliday 일반 물리학 9th ed